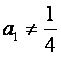 ,且
,且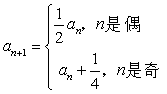 ,记
,记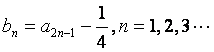
解答题
(19)(本小题共12分)
设数列![]() 的首项
的首项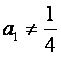 ,且
,且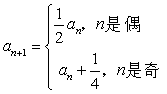 ,记
,记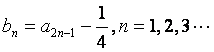
![]()
(Ⅰ)求![]()
(Ⅱ)判断数列![]() 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(Ⅲ)求![]()
![]()
解:(I)a2=a1+![]() =a+
=a+![]() ,a3=
,a3=![]() a2=
a2=![]() a+
a+![]() ;
;
(II)∵ a4=a3+![]() =
=![]() a+
a+![]() ,
所以a5=
,
所以a5=![]() a4=
a4=![]() a+
a+![]() ,
,
所以b1=a1-![]() =a-
=a-![]() ,
b2=a3-
,
b2=a3-![]() =
=![]() (a-
(a-![]() ),
b3=a5-
),
b3=a5-![]() =
=![]() (a-
(a-![]() ),
),
猜想:{bn}是公比为![]() 的等比数列·
的等比数列·
证明如下:
因为bn+1=a2n+1-![]() =
=![]() a2n-
a2n-![]() =
=![]() (a2n-1-
(a2n-1-![]() )=
)=![]() bn,
(n∈N*)
bn,
(n∈N*)
所以{bn}是首项为a-![]() ,
公比为
,
公比为![]() 的等比数列
的等比数列![]()
(III)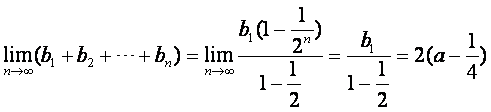
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。