解答题
(21) (本小题满分12分)已知数列![]() 的首项
的首项![]() 前
前![]() 项和为
项和为![]() ,
,
且![]()
(I)证明数列![]() 是等比数列;
是等比数列;
(II)令![]() ,求函数
,求函数![]() 在点
在点![]() 处的导数
处的导数![]()
并比较![]() 与
与![]() 的大小
的大小![]()
(考查知识点:数列)
解:由已知![]() 可得
可得![]() 两式相减得
两式相减得
![]() 即
即![]() 从而
从而![]() 当
当![]() 时
时
![]() 所以
所以![]() 又
又![]() 所以
所以![]() 从而
从而![]()
故总有![]() ,
,![]() 又
又![]() 从而
从而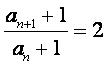
即数列![]() 是等比数列;
是等比数列;
(II)由(I)知![]()
因为![]() 所以
所以![]()
从而![]() =
=![]()
=![]() -
-![]() =
=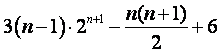
由上![]() -
-![]() =
=
![]() =12
=12![]() ①
①
当![]() 时,①式=0所以
时,①式=0所以![]() ;
;
当![]() 时,①式=-12
时,①式=-12![]() 所以
所以![]()
当![]() 时,
时,![]() 又
又![]()
![]()
![]()
所以![]() 即①
即①![]() 从而
从而![]()
![]()
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。