解答题

20．（本小题满分14分）

自然状态下的鱼类是一种可再生资源，为持续利用这一资源，需从宏观上考察

其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量，

n∈N*，且x1＞0.不考虑其它因素，设在第n年内鱼群的繁殖量及捕捞量都与xn成

正比，死亡量与xn2成正比，这些比例系数依次为正常数a，b，c.

   （Ⅰ）求xn+1与xn的关系式；

   （Ⅱ）猜测：当且仅当x1，a，b，c满足什么条件时，每年年初鱼群的总量

保持不变？（不要求证明）

　 （Ⅱ）设a＝2，b＝1，为保证对任意x1∈（0,2），都有xn＞0，n∈N*，

则捕捞强度b的最大允许值是多少？证明你的结论.

 解:

（I）从第n年初到第n+1年初，鱼群的繁殖量为ax_n，被捕捞量为bx_n，死亡量为

   （II）若每年年初鱼群总量保持不变，则xn恒等于x1， n∈N*，从而由（*）式得

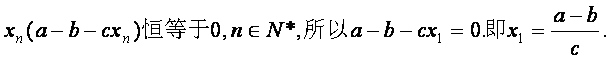
        因为x1>0，所以a>b

        猜测：当且仅当a>b，且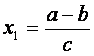时，每年年初鱼群的总量保持不变

   （Ⅲ）若b的值使得x_n>0，n∈N*

         由x_n+1=x_n(3－b－x_n), n∈N*, 知

         0<x_n<3－b, n∈N*, 特别地，有0<x₁<3－b. 即0<b<3－x₁.

        而x₁∈(0, 2)，所以

        由此猜测b的最大允许值是1

        下证 当x₁∈(0, 2) ，b=1时，都有x_n∈(0, 2), n∈N*

        ①当n=1时，结论显然成立

        ②假设当n=k时结论成立，即x_k∈(0, 2),

        则当n=k+1时，x_k+1=x_k(2－x_k­)>0.

        又因为x_k+1=x_k(2－x_k)=－(x_k－1)2+1≤1<2,

        所以x_k+1∈(0, 2)，故当n=k+1时结论也成立.

        由①、②可知，对于任意的n∈N*，都有x_n∈(0,2).

   综上所述，为保证对任意x₁∈(0, 2), 都有x_n>0， n∈N*，

   则捕捞强度b的最大允许值是1.