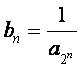解答题

（18） （本小题满分12分）

已知是各项均为正数的等差数列，、、成等差数列．又，…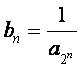

（Ⅰ）证明为等比数列；

（Ⅱ）如果无穷等比数列各项的和，求数列的首项和公差．

（注：无穷数列各项的和即当时数列前项和的极限）

本小题主要考查等差数列、等比数列的基本知识以及运用这些知识的能力

⑴证明：设{an}中首项为a1，公差为d.

∵lga1,lga2,lga4成等差数列  ∴2lga2=lga1·lga4   ∴a22=a1·a4.

即(a1+d)2=a1(a1+3d)   ∴d=0或d=a1

当d=0时, an=a1, bn=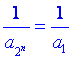, ∴，∴为等比数列；

当d=a1时, an=na1 ,bn=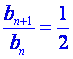，∴，∴为等比数列

综上可知为等比数列

⑵∵无穷等比数列{bn }各项的和

∴|q|<1, 由⑴知，q=, d=a1 . bn=

∴, ∴a1=3

∴