解答题
20.设点![]() (
(![]() ,0),
,0),![]() 和抛物线
和抛物线![]() :y=x2+an x+bn(n∈N*),其中
:y=x2+an x+bn(n∈N*),其中
an=-2-4n-![]() ,
,![]() 由以下方法得到:
由以下方法得到:
x1=1,点P2(x2,2)在抛物线C1:y=x2+a1x+b1上,点A1(x1,0)到P2的距离是
A1到C1上点的最短距离,…,点![]() 在抛物线
在抛物线![]() :y=x2+an x+bn上,
:y=x2+an x+bn上,
点![]() (
(![]() ,0)到
,0)到![]() 的距离是
的距离是![]() 到
到![]() 上点的最短距离.
上点的最短距离.
(Ⅰ)求x2及C1的方程.
(Ⅱ)证明{![]() }是等差数列.
}是等差数列.
本题主要考查二次函数的求导、导数的应用、等差数列、数学归纳法等基础知识,
以及综合运用所学知识分析和解决问题的能力![]() 满分14分
满分14分![]()
解:(Ⅰ)由题意得![]() ,
,
设点![]() 是
是![]() 上任意一点,
上任意一点,
则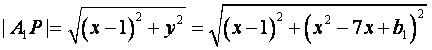
令![]()
则![]()
由题意得![]() ,
,
即![]()
又![]() 在
在![]() 上,
上,![]()
解得![]()
故![]() 的方程为
的方程为![]()
(Ⅱ)设点![]() 是
是![]() 上任意一点,
上任意一点,
则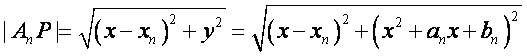
令![]()
![]()
则![]()
由题意得![]()
即![]()
又![]() ,
,
![]() ,
,
即![]()
下面用数学归纳法证明![]() ,
,
①当![]() 时,
时,![]() ,等式成立;
,等式成立;
②假设当![]() 时,等式成立,即
时,等式成立,即![]() ,
,
则当![]() 时,由
时,由![]() 知
知![]() ,
,
又 ,
, ,
,
即![]() 时,等式成立
时,等式成立![]()
由①②知,等式对![]() 成立,
成立,
故![]() 是等差数列
是等差数列![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。