2004年

解答题

17、(本题满分12分)

    已知复数z₁满足(1+i)z­₁=－1+5i, z­₂=a－2－i, 其中i为虚数单位,

a∈R, 若<,求a的取值范围.

  解答

18、(本题满分12分)

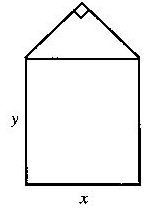  某单位用木料制作如图所示的框架, 框架的下部是边长分别为

  x、y(单位：m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm².

  问x、y分别为多少(精确到0.001m) 时用料最省?

     解答

19、(本题满分14分) 第1小题满分6分, 第2小题满分8分

  记函数f(x)=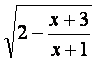的定义域为A, g(x)=lg[(x－a－1)(2a－x)](a<1)

 的定义域为B.

(1) 求A；

(2) 若BA, 求实数a的取值范围.

 解答

20、(本题满分14分) 第1小题满分6分, 第2小题满分8分

  已知二次函数y=f₁(x)的图象以原点为顶点且过点(1,1),反比例函数

y=f₂(x)的图象与直线y=x的两个交点间距离为8,f(x)= f₁(x)+ f₂(x).

 (1) 求函数f(x)的表达式；

 (2) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.

 解答

21、(本题满分16分) 第1小题满分4分, 第2小题满分6分, 第3小题满分6分

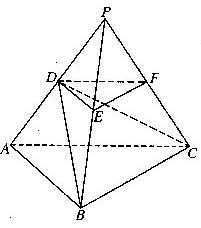  如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上

的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.

(棱长和是指多面体中所有棱的长度之和)

(1)     证明：P-ABC为正四面体；

(2)     若PD=PA, 求二面角D-BC-A的

大小；(结果用反三角函数值表示)

(3)     设棱台DEF-ABC的体积为V, 是

否存在体积为V且各棱长均相等的直

平行六面体,使得它与棱台DEF-ABC

有相同的棱长和? 若存在,请具体构造

出这样的一个直平行六面体,并给出证

明；若不存在,请说明理由.

  解答

22、(本题满分18分) 第1小题满分6分, 第2小题满分4分, 第3小题满分8分

  设P₁(x₁,y₁), P₁(x₂,y₂),…, P_n(x_n,y_n)(n≥3,n∈N) 是二次曲线C上

的点, 且a₁=², a₂=², …, a_n=²构成了一个公差为d(d≠0) 的

等差数列, 其中O是坐标原点. 记S_n=a₁+a₂+…+a_n.

(1)      若C的方程为=1,n=3. 点P₁(3,0) 及S₃=255, 求点P₃的坐标；

 (只需写出一个)

(2)若C的方程为(a>b>0). 点P₁(a,0), 对于给定的自然数n, 当公

差d变化时, 求S_n的最小值；

. (3)请选定一条除椭圆外的二次曲线C及C上的一点P₁,对于给定的自然数n,

写出符合条件的点P₁, P₂,…P_n存在的充要条件,并说明理由.

 解答

2005年

解答题

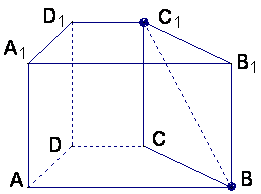
17.已知直四棱柱中，，底面是直角梯形，

，，，，，求异面直线与

所成的角的大小（结果用反三角函数表示）

解答

18.证明：在复数范围内，方程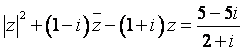（为虚数单位）无解

解答

19.点A、B分别是椭圆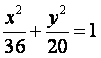长轴的左、右焦点，点F是椭圆的右焦点点P在椭圆上，

且位于x轴上方，

（1）求P点的坐标；

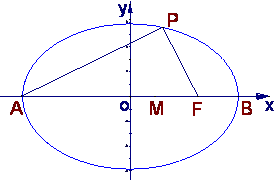    （2）设M是椭圆长轴AB上的一点，M到直线AP的

     距离等于，求椭圆上的点到点M的距离d的最小值

解答

20.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分

假设某市2004年新建住房400万平方米，其中有250万平方米是中低价房预计

在今后的若干年内，该市每年新建住房面积平均比上一年增长8%，另外，每年新

建住房中，中低价房的面积均比上一年增加50万平方米那么，到那一年底，

（1）该市历年所建中低价房的累计面积（以2004年为累计的第一年）将首次不少

于4750万平方米？

（2）当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%？

解答

21.（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分8分，

第3小题满分6分

对定义域是.的函数.，

规定：函数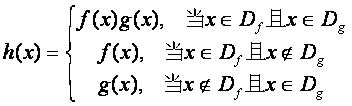

（1）若函数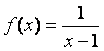，，写出函数的解析式；

（2）求问题（1）中函数的值域；

（3）若，其中是常数，且，请设计一个定义域为R的函数

，及一个的值，使得，并予以证明

解答

22.在直角坐标平面中，已知点，，，，其中

n是正整数对平面上任一点，记为关于点的对称点，为关于点的

对称点，为关于点的对称点

（1）求向量的坐标；

（2）当点在曲线C上移动时，点的轨迹是函数的图像，其中是

以3位周期的周期函数，且当时，求以曲线C为图像的函数

在上的解析式；

（3）对任意偶数n，用n表示向量的坐标

解答

2006

解答题

17．（本题满分12分）

求函数＝2＋的值域和最小正周期．

解答

18．（本题满分12分）

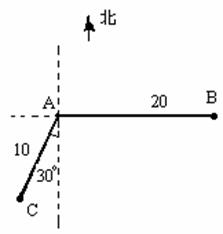
如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘

渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南

偏西30，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向

沿直线前往B处救援（角度精确到1）？

解答

19．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分）

在四棱锥P－ABCD中，底面是边长为2的菱形，∠DAB＝60，对角线AC与BD

相交于点O，PO⊥平面ABCD，PB与平面ABCD所成的角为60．

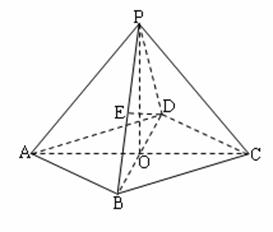
（1）求四棱锥P－ABCD的体积；

（2）若E是PB的中点，求异面直线DE与PA所成角的大小（结果用反三角函数值表示）．

解答

20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分）

在平面直角坐标系O中，直线与抛物线＝2相交于A、B两点．

（1）求证：“如果直线过点T（3，0），那么＝3”是真命题；

（2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由．

 解答

21．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，

第3小题满分6分）

已知有穷数列共有2项（整数≥2），首项＝2．设该数列的前项

和为，且＝＋2（＝1，2，┅，2－1），其中常数＞1．

（1）求证：数列是等比数列；

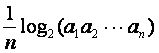（2）若＝2，数列满足＝（＝1，2，┅，2），

求数列的通项公式；

（3）若（2）中的数列满足不等式

|－|＋|－|＋┅＋|－|＋|－|≤4，求的值．

 解答

22．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，

第3小题满分9分）

已知函数＝＋有如下性质：如果常数＞0，那么该函数在

0，上是减函数，在，＋∞上是增函数．

（1）如果函数＝＋（＞0）的值域为6，＋∞，求的值；

（2）研究函数＝＋（常数＞0）在定义域内的单调性，并说明理由；

（3）对函数＝＋和＝＋（常数＞0）作出推广，使它们都是

你所推广的函数的特例．研究推广后的函数的单调性（只须写出结论，不必

证明），并求函数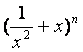＝＋（是正整数）在区间[，2]上

的最大值和最小值（可利用你的研究结论）．

 解答

2007年

解答题

16．（本题满分12分）

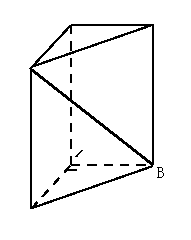    如图，在体积为1的直三棱柱中，

．

求直线与平面所成角的大小

（结果用反三角函数值表示）．

解答

17．（本题满分14分）

   在中，分别是三个内角的对边．若，，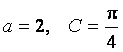

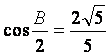求的面积．

解答

18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．

    近年来，太阳能技术运用的步伐日益加快．2002年全球太阳电池的年生产量

达到670兆瓦，年生产量的增长率为34%．以后四年中，年生产量的增长率逐年递

增2%（如，2003年的年生产量的增长率为36%）．

   （1）求2006年全球太阳电池的年生产量（结果精确到0.1兆瓦）；

   （2）目前太阳电池产业存在的主要问题是市场安装量远小于生产量，2006年

的实际安装量为1420兆瓦．假设以后若干年内太阳电池的年生产量的增长率保持

在42%，到2010年，要使年安装量与年生产量基本持平（即年安装量不少于年生产

量的95%），这四年中太阳电池的年安装量的平均增长率至少应达到多少（结果精

确到0.1%）？

解答

19．（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．

     已知函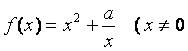数，常数．

    （1）讨论函数的奇偶性，并说明理由；

    （2）若函数在上为增函数，求的取值范围．

解答

20．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，

第3小题满分9分．

    如果有穷数列（为正整数）满足条件，，

…，，即（），我们称其为“对称数列”．例如，

由组合数组成的数列就是“对称数列”．

（1）设是项数为7的“对称数列”，其中是等差数列，且，

．依次写出的每一项；

（2）设是项数为(正整数)的“对称数列”，其中是

首项为，公差为的等差数列．记各项的和为．当为何值时，

取得最大值？并求出的最大值；

（3）对于确定的正整数，写出所有项数不超过的“对称数列”，

使得依次是该数列中连续的项；当时，求其中一个

“对称数列”前项的和．

解答

21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，

第3小题满分8分．

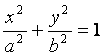
我们把由半椭圆 与半椭圆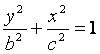 合成的曲线称作“果圆”，

其中，，．

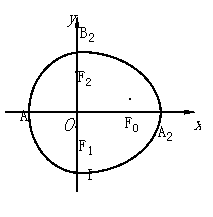如图，点，，是相应椭圆的焦点，，和，分别是“果圆”与，轴的交点．

（1）若是边长为1的等边三角形，求

“果圆”的方程；

    （2）当时，求的取值范围；

（3）连接“果圆”上任意两点的线段称为“果圆”

的弦．试研究：是否存在实数，使斜率为的“果圆”

平行弦的中点轨迹总是落在某个椭圆上？若存在，求出所有可能的值；

若不存在，说明理由．

解答