 (a,b为常数)且方程f(x)-x+12=0有两个实根
(a,b为常数)且方程f(x)-x+12=0有两个实根2005年
解答题
17.(本小题满分12分)
已知函数 (a,b为常数)且方程f(x)-x+12=0有两个实根
(a,b为常数)且方程f(x)-x+12=0有两个实根
为x1=3, x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;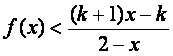
18.(本小题满分12分)
已知向量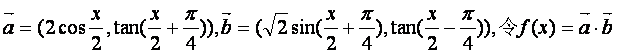 .
.
求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.
19.(本小题满分12分)
A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝
上时A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏
终止.求掷硬币的次数不大于7次时游戏终止的概率.
20.(本小题满分12分)
如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
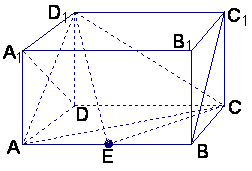 (3)AE等于何值时,二面角D1—EC—D的大小为
(3)AE等于何值时,二面角D1—EC—D的大小为![]() .
.
21.(本小题满分12分)
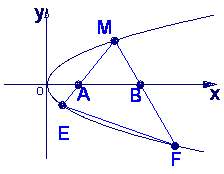
如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹方程.
22.(本小题满分14分)
已知数列{an}的前n项和Sn满足Sn-Sn-2=3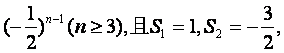
求数列{an}的通项公式.
2006
解答题17.(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
18.(本小题满分12分)
某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中
每次随机地摸出一个球,记下颜色后放回,摸出一个红球获得二等奖;摸出两个
红球获得一等奖.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次.求
(1)甲、乙两人都没有中奖的概率;
(2)甲、乙两人中至少有一人获二等奖的概率.
19.(本小题满分12分)
在锐角△ABC中,角A、B、C所对的边分别为a、b、c,已知sinA=![]() ,
,
(1)求tan2![]() +sin2
+sin2![]() 的值;
的值;
(2)若a=2,S△ABC=![]() ,求b的值.
,求b的值.
20.(本小题满分12分)
如图,已知三棱锥O-ABC的侧棱OA、OB、OC两两垂直,且OA=1,OB=OC=2,
E是OC的中点.
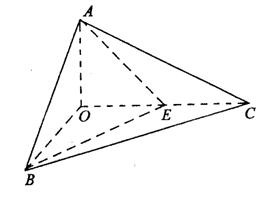
(1)求O点到面ABC的距离;
(2)求异面直线BE与AC所成的角;
(3)求二面角E-AB-C的大小.
21.(本小题满分12分)
如图,椭圆Q: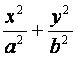 =1(a>b>0)的右焦点为F(c,0),过点F的一动直线m
=1(a>b>0)的右焦点为F(c,0),过点F的一动直线m
绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令a2=1+cosθ+sinθ,b2=sinθ(0<θ≤![]() ).
).
设轨迹H的最高点和最低点分别为M和N.当θ为何值时,△MNF为—个正三角形?
22.(本小题满分14分)
已知各项均为正数的数列{an}满足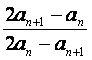 =anan+1,n∈N*.
=anan+1,n∈N*.
(1)求数列{an}的通项公式;
(2)设Sn=a21+a22+…+a2n,Tn=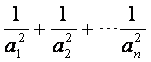 ,求Sn+Tn,并确定最小正整数
,求Sn+Tn,并确定最小正整数
n,使Sn+Tn为整数.
2007年
解答题
17.(本小题满分12分)
已知函数 满足
满足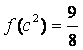 .
.
(1)求常数![]() 的值;
的值;
(2)解不等式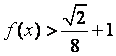 .
.
18.(本小题满分12分)
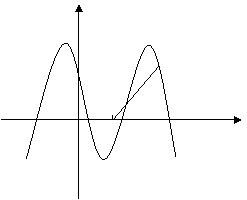 如图,函数
如图,函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,
,
且该函数的最小正周期为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
![]()
(2)已知点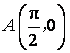 ,点
,点![]() 是该函数图象
是该函数图象
上一点,点![]() 是
是![]() 的中点,
的中点,
当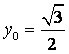 ,
, 时,求
时,求![]() 的值.
的值.
19.(本小题满分12分)
栽培甲、乙两种果树,先要培育成苗,然后再进行移栽.已知甲、乙两种果树
成苗的概率分别为![]() ,
,![]() ,移栽后成活的概率分别为
,移栽后成活的概率分别为![]() ,
,![]() .
.
(1)求甲、乙两种果树至少有一种果树成苗的概率;
(2)求恰好有一种果树能培育成苗且移栽成活的概率.
20.(本小题满分12分)
 右图是一个直三棱柱(以
右图是一个直三棱柱(以![]() 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为![]() .
.
已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)设点![]() 是
是![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(3)求此几何体的体积.
21.(本小题满分12分)
设![]() 为等比数列,
为等比数列,![]() ,
,![]() .
.
(1)求最小的自然数![]() ,使
,使![]() ;
;
(2)求和: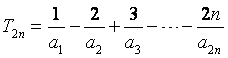 .
.
22.(本小题满分14分)
设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,
,
且存在常数![]() ,使得
,使得![]() .
.
 (1)证明:动点
(1)证明:动点![]() 的轨迹
的轨迹![]() 为双曲线,并求出
为双曲线,并求出![]() 的方程;
的方程;
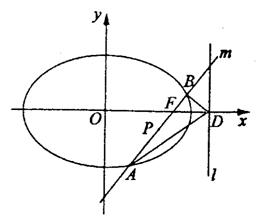
(2)如图,过点![]() 的直线与双曲线
的直线与双曲线![]() 的右支交于
的右支交于![]() 两点.
两点.
问:是否存在![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰
为直角顶点的等腰
直角三角形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。