2004年

解答题

(17)(本小题满分12分)

   已知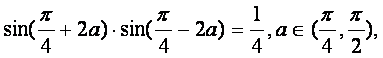求的值.

  解答

(19) (本小题满分12分)

如图,在底面是菱形的四棱锥P—ABCD中,

     点E在PD上,且PE:ED= 2: 1.

     (Ⅰ)证明 PA⊥平面ABCD;

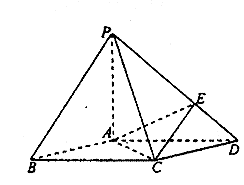(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小:

(Ⅲ)在棱PC上是否存在一点F, 使BF∥平面AEC?证明你的结论.

                                  解答

(20)(本小题满分12分)

已知函数其中a≤0,e为自然对数的底数.

  (Ⅰ)讨论函数f(x)的单调性;

(Ⅱ)求函数f(x)在区间[0,1]上的最大值.

 解答

(21)(本小题满分12分)

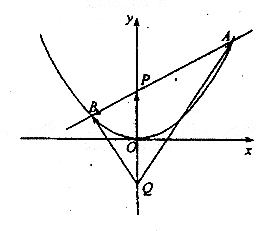
 如图,过抛物线x²=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线

交于A、B两点，点Q是点P关于原点的对称点。

  (Ⅰ)设点P分有向线段所成的比为λ，证明

(Ⅱ)设直线AB的方程是x—2y+12=0,过A、B两点的圆C与抛物线在点A处

有共同的切线，求圆C的方程。

                                             解答

（22）（本小题满分14分）

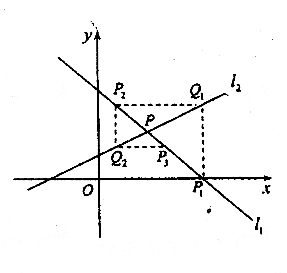
如图，直线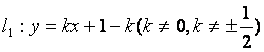与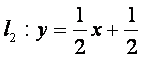相交于点P。直线

与x轴交于点P₁，过点P₁作x轴的垂线交直线于点Q₁，过点Q₁作y轴的

垂线交直线于点P₂，过点P₂作x轴的垂线交直线于点Q₂，…，这样

一直作下去，可得到一系列点P₁，Q₁，P₂，Q₂，…。点P_n（n=1,2,…）

的横坐标构成数列。

  (Ⅰ)证明

(Ⅱ)求数列的通项公式；

(Ⅲ)比较与的大小。

 解答

2005年

解答题

16．（本小题满分12分）

已知在△ABC中，sinA（sinB＋cosB）－sinC＝0，sinB＋cos2C＝0，

求角A、B、C的大小.

解答

17．（本题满分12分）

　  如图1，已知ABCD是上．下底边长分别为2和6，高为的等腰梯形，

    将它沿对称轴OO1折成直二面角，如图2.

　　（Ⅰ）证明：AC⊥BO1；

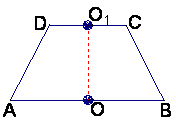
 （Ⅱ）求二面角O－AC－O1的大小.

       解答                                               图1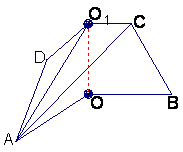                 图2

18．（本小题满分14分）

某城市有甲、乙、丙3个旅游景点，一位客人游览这三个景点的概率分别

是0.4，0.5，0.6，且客人是否游览哪个景点互不影响，设ξ表示客人离开

该城市时游览的景点数与没有游览的景点数之差的绝对值.

（Ⅰ）求ξ的分布及数学期望；

（Ⅱ）记“函数f(x)＝x²－3ξx＋1在区间[2，＋∞上单调递增”为

事件A，求事件A的概率. 

解答

19．（本小题满分14分）

已知椭圆C：＋＝1（a＞b＞0）的左．右焦点为F1、F2，离心率为e.

直线l：y＝ex＋a与x轴．y轴分别交于点A、B，M是直线l与椭圆C的一个公

共点，P是点F1关于直线l的对称点，设＝λ.

   （Ⅰ）证明：λ＝1－e2；

   （Ⅱ）确定λ的值，使得△PF1F2是等腰三角形.

解答

20．（本小题满分14分）

自然状态下的鱼类是一种可再生资源，为持续利用这一资源，需从宏观上考察

其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量，

n∈N*，且x1＞0.不考虑其它因素，设在第n年内鱼群的繁殖量及捕捞量都与xn成

正比，死亡量与xn2成正比，这些比例系数依次为正常数a，b，c.

   （Ⅰ）求xn+1与xn的关系式；

   （Ⅱ）猜测：当且仅当x1，a，b，c满足什么条件时，每年年初鱼群的总量

保持不变？（不要求证明）

　 （Ⅱ）设a＝2，b＝1，为保证对任意x1∈（0,2），都有xn＞0，n∈N*，

则捕捞强度b的最大允许值是多少？证明你的结论.

解答

21．（本小题满分14分）

    已知函数f(x)＝lnx，g(x)＝ax2＋bx，a≠0

   （Ⅰ）若b＝2，且h(x)＝f(x)－g(x)存在单调递减区间，求a的取值范围；

   （Ⅱ）设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q，过线段PQ的中

    点作x轴的垂线分别交C1，C2于点M、N，证明C1在点M处的切线与C2在点N

    处的切线不平行

解答

2006

解答题

16．（本小题满分12分）

如图3，D是直角△ABC斜边BC上一点，AB=AD，记∠CAD=α，∠ABC=β.

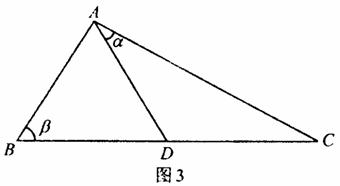
（Ⅰ）证明：sinα+cos2β=0；

（Ⅱ）若AC=DC，求β的值.

解答

17．(本小题满分12分)

    某安全生产监督部门对5家小型煤矿进行安全检查(简称安检)．若安检不合格，

则必须整改．若整改后经复查仍不合格，则强制关闭．设每家煤矿安检是否合格

是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率

是0.8，计算(结果精确到0.01)：

    (Ⅰ)恰好有两家煤矿必须整改的概率；

    (Ⅱ)平均有多少家煤矿必须整改；

    (Ⅲ)至少关闭一家煤矿的概率．

解答

18．(本小题满分14分)

    如图4，己知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2，AB=4．

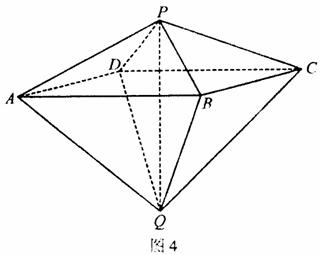
    (Ⅰ)证明PQ⊥平面ABCD；

    (Ⅱ)求异面直线AQ与PB所成的角；

    (Ⅲ)求点P到平面QAD的距离．

解答     

19．(本小题满分14分)

已知函数f(x)=x-sinx，数列{a_n}满足：0＜a₁＜1，a_n+1=f(a_n)，n=1，2，3，…．

证明：(Ⅰ)0＜a_n+1＜a_n＜1；(Ⅱ)a_n+1＜a_n³．

解答

20．(本小题满分14分)

对1个单位质量的含污物体进行清洗，清洗前其清洁度(含污物体的清洁度定义为：

1-)为0.8，要求洗完后的清洁度是0.99．有两种方案可供选择，方案

甲：一次清洗；方案乙：分两次清洗．该物体初次清洗后受残留水等因素影响，其

质量变为a(1≤a≤3)．设用x单位质量的水初次清洗后的清洁度是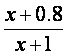(x＞a-1)，用

y单位质量的水第二次清洗后的清洁度是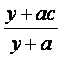，其中c(0.8＜c＜0.99)是该物体初次清

洗后的清洁度．

(Ⅰ)分别求出方案甲以及c=0.95时方案乙的用水量，并比较哪一种方案用水量较少；

(Ⅱ)若采用方案乙，当a为某定值时，如何安排初次与第二次清洗的用水量，使总用水

量最少?并讨论a取不同数值时对最少总用水量多少的影响．

解答

21.(本小题满分14分)

已知椭圆C₁: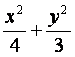=1，抛物线C₂:(y-m)²=2px(p＞0)，且C₁、C₂的公共弦AB过椭圆

C₁的右焦点.

(Ⅰ)当AB⊥x轴时，求m、p的值，并判断抛物线C₂的焦点是否在直线AB上；

(Ⅱ)是否存在m、p的值，使抛物线C₂的焦点恰在直线AB上?若存在，求出符合条件的

m、p的值；若不存在，请说明理由．

解答

2007年

解答题

16．（本小题满分12分）

已知函数，．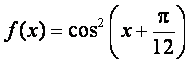

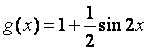（I）设是函数图象的一条对称轴，求的值．

（II）求函数的单调递增区间．

解答

17．（本小题满分12分）

某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力，

每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训，已知参加

过财会培训的有60%，参加过计算机培训的有75%，假设每个人对培训项目的选

择是相互独立的，且各人的选择相互之间没有影响．

（I）任选1名下岗人员，求该人参加过培训的概率；

（II）任选3名下岗人员，记为3人中参加过培训的人数，求的分布列和期望．

解答

18．（本小题满分12分）

如图2，分别是矩形的边的中点，是上的一点，将，

分别沿翻折成，，并连结，使得平面平面，

，且．连结，如图3．

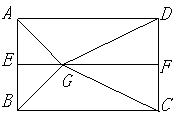
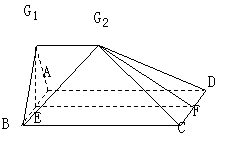
　　　　图2                             图3

（I）证明：平面平面；

（II）当，，时，求直线和平面所成的角．

解答

19．（本小题满分12分）

如图4，某地为了开发旅游资源，欲修建一条连接风景点和居民区的公路，

点所在的山坡面与山脚所在水平面所成的二面角为（），且，

点到平面的距离（km）．沿山脚原有一段笔直的公路可供利用．

从点到山脚修路的造价为万元/km，原有公路改建费用为万元/km．当山坡上

公路长度为km（）时，其造价为万元．已知，，

，．

（I）在上求一点，使沿折线修建公路的总造价最小；

（II） 对于（I）中得到的点，在上求一点，使沿折线修建公路的

总造价最小．

（III）在上是否存在两个不同的点，，使沿折线修建公路的总造

价小于（II）中得到的最小总造价，证明你的结论．

解答

20．（本小题满分12分）

已知双曲线的左、右焦点分别为，，过点的动直线与双曲线

相交于两点．

（I）若动点满足（其中为坐标原点），求点的轨迹方程；

（II）在轴上是否存在定点，使·为常数？若存在，求出点的坐标；

若不存在，请说明理由．

解答

21．（本小题满分13分）

已知（）是曲线上的点，，是数列的前项和，

且满足，，…．

（I）证明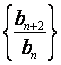：数列（）是常数数列；

（II）确定的取值集合，使时，数列是单调递增数列；

（III）证明：当时，弦（）的斜率随单调递增．

解答