三、解答题

19．（本小题满分12分）

如图4，某地为了开发旅游资源，欲修建一条连接风景点和居民区的公路，

点所在的山坡面与山脚所在水平面所成的二面角为（），且，

点到平面的距离（km）．沿山脚原有一段笔直的公路可供利用．

从点到山脚修路的造价为万元/km，原有公路改建费用为万元/km．当山坡上

公路长度为km（）时，其造价为万元．已知，，

，．

（I）在上求一点，使沿折线修建公路的总造价最小；

（II） 对于（I）中得到的点，在上求一点，使沿折线修建公路的

总造价最小．

（III）在上是否存在两个不同的点，，使沿折线修建公路的总造

价小于（II）中得到的最小总造价，证明你的结论．

解：（I）如图，，，，

由三垂线定理逆定理知，，所以是

山坡与所成二面角的平面角，则，

．

设，．则

．

记总造价为万元，

据题设有

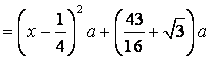
当，即时，总造价最小．

（II）设，，总造价为万元，根据题设有

．

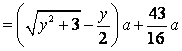则，由，得．

当时，，在内是减函数；

当时，，在内是增函数．

故当，即（km）时总造价最小，且最小总造价为万元．

（III）解法一：不存在这样的点，．

事实上，在上任取不同的两点，．为使总造价最小，显然不能位

于 与之间．故可设位于与之间，且=，，

，总造价为万元，则．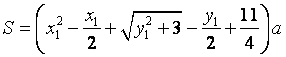

类似于（I）、（II）讨论知，，，当且仅当，

同时成立时，上述两个不等式等号同时成立，此时，，

取得最小值，点分别与点重合，所以不存在这样的点 ，

使沿折线修建公路的总造价小于（II）中得到的最小总造价．

解法二：同解法一得

．

当且仅当且，即同时成立时，

取得最小值，以上同解法一．