解答题

全国卷Ⅰ(理)

18．（本小题满分12分）

一接待中心有A、B、C、D四部热线电话，已知某一时刻电话A、B占线的

概率均为0.5，电话C、D占线的概率均为0.4，各部电话是否占线相互之间

没有影响.假设该时刻有ξ部电话占线.试求随机变量ξ的概率分布和它的期望.

解答

全国卷Ⅱ(理)

18．（本小题满分12分）

       已知8支球队中有3支弱队，以抽签方式将这8支球队分为A、B两组，每组4支.

求：（Ⅰ）A、B两组中有一组恰有两支弱队的概率；

    （Ⅱ）A组中至少有两支弱队的概率.

解答

全国卷Ⅲ(理)

18．（本小题满分12分）解方程   .

解答

全国卷Ⅳ(理)

18．（本小题满分12分）

       求函数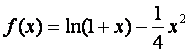在[0，2]上的最大值和最小值.

 解答

天津卷(理)

18. （本小题满分12分）

  从4名男生和2名女生中任选3人参加演讲比赛，设随机变量表示

所选3人中女生的人数。

  （1）求的分布列；

（2）求的数学期望；

（3）求“所选3人中女生人数”的概率。

  解答

辽宁卷

18．（本小题满分12分）

设全集U=R

（1）解关于x的不等式

       
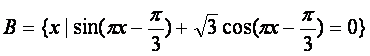        若（  _∪A）∩B恰有3个元素，求a的取值范围.

      解答

江苏卷

    18.在棱长为4的正方体ABCD-A₁B₁C₁D₁中，O是正方形A₁B₁C₁D₁的中心，

    点P在棱CC₁上，且CC₁=4CP.

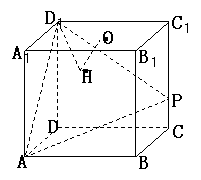    (Ⅰ)求直线AP与平面BCC₁B₁所成的角的大小（结果用反三角函数值表示）；

    (Ⅱ)设O点在平面D₁AP上的射影是H，求证：D₁H⊥AP；

    (Ⅲ)求点P到平面ABD₁的距离.

     解答

浙江卷(理)

（18） （本题满分12分）

盒子中有大小相同的球10个，其中标号为1的球3个，标号为2的球4个，

标号为5的球3个，第一次从盒子中任取1个球，放回后第二次再任取1个球

（假设取到每个球的可能性都相同）。记第一次与第二次取到球的标号之和为ε。

（Ⅰ）求随机变量ε的分布列；

（Ⅱ）求随机变量ε的期望Eε。

解答

福建卷(理)

（18）（本小题满分12分）

甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能

答对其中的6题，乙能答对其中的8题。规定每次考试都从备选题中随

机抽出3题进行测试，至少答对2题才算合格。

（Ⅰ）求甲答对试题数ξ的概率分布及数学期望；

（Ⅱ）求甲、乙两人至少有一人考试合格的概率。

 解答

湖北卷(理)

（18）（本小题满分12分）

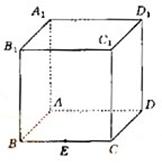如图，在棱长为1的正方体ABCD－A₁、B₁、C₁、D₁中，点E是棱BC的中点，

点F 是棱CD上的动点。

（Ⅰ）试确定点F的位置，使得D₁E⊥平面AB₁F；

（Ⅱ）当D₁E⊥平面AB₁F时，求二面角C₁―EF―A的大小

（结果用反三角函数值表示）。

                          解答

重庆卷(理)

18．（本小题满分12分）

设一汽车在前进途中要经过4个路口，汽车在每个路口遇到绿灯的

概率为，遇到红灯（禁止通行）的概率为。假定汽车只在遇到

红灯或到达目的地才停止前进，表示停车时已经通过的路口数，求：

（1）的概率的分布列及期望E;

 (2 )  停车时最多已通过3个路口的概率。

解答

北京卷(理)

（16）（本小题满分14分）

    如图，在正三棱柱中，AB＝3，，M为的中点，P是BC上一点，

且由P沿棱柱侧面经 过棱到M的最短路线长为，设这条最短路线与的交点为N，

求：

    （I）该三棱柱的侧面展开图的对角线长

    （II）PC和NC的长

    （III）平面NMP与平面ABC所成二面角（锐角）的大小（用反三角函数表示）

解答

上海卷(理)

18、(本题满分12分)

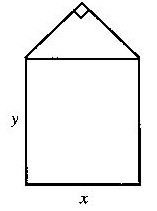  某单位用木料制作如图所示的框架, 框架的下部是边长分别为

  x、y(单位：m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm².

  问x、y分别为多少(精确到0.001m) 时用料最省?

     解答

广东卷

18. (12分)如右下图,在长方体ABCD—A₁B₁C₁D₁中,已知AB= 4, AD =3, AA₁= 2.

E、F分别是线段AB、BC上的点，且EB= FB=1.

(1) 求二面角C—DE—C₁的正切值;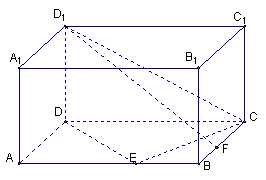

(2) 求直线EC₁与FD₁所成的余弦值.

解答