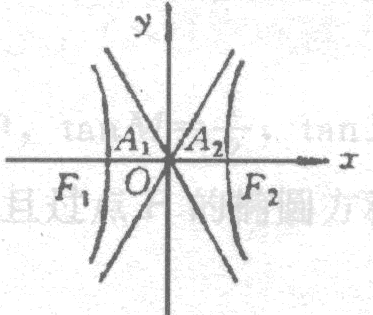一、高考大纲
考试内容:
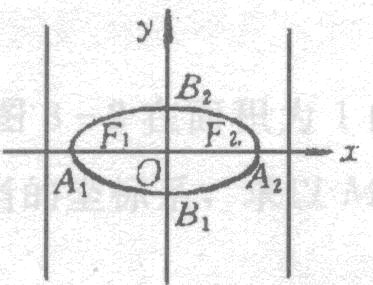
椭圆及其标准方程。椭圆的简单几何性质。椭圆的参数方程。
双曲线及其标准方程。双曲线的简单几何性质。
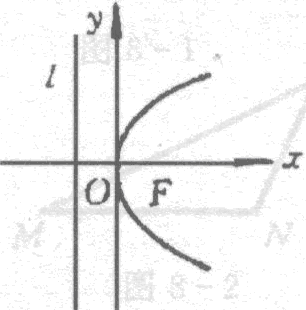
抛物线及其标准方程。抛物线的简单几何性质。。
考试要求:
(1)掌握椭圆的定义、标准方程和椭圆的简单几何性质,了解椭圆的参数方程。
(2)掌握双曲线的定义、标准方程和双曲线的简单几何性质。
(3)掌握抛物线的定义、标准方程和抛物线的简单几何性质。
(4)了解圆锥曲线的初步应用。
二、高考要览
| 考试内容 |
能力层次 |
高考要求 |
考题年份分值 |
| 椭圆 |
熟练 掌握 |
椭圆的标准方程及其几何性质 |
|
2004 |
2005 |
2006 |
2007 |
2008 |
| 全国Ⅱ.4 |
|
全国Ⅱ5.5 |
|
|
| |
山东.5 |
山东7.5 |
|
|
| |
辽宁.14 |
辽宁8.5 |
|
|
|
上海春.4 |
上海.4 |
上海7.4 |
|
|
| |
|
四川15.4 |
|
|
|
湖北.5 |
湖北.12 |
湖北20.14 |
|
|
| |
|
江西21.12 |
|
|
|
安徽春.5 |
|
安徽3.5 |
|
|
|
重庆.4 |
重庆.5 |
|
|
|
| |
江苏.5 |
|
|
|
|
浙江.5 |
浙江.14 |
|
|
|
|
福建.5 |
福建.12 |
|
|
|
|
湖南.4 |
湖南.14 |
|
|
|
|
北京春.4 |
北京春.5 |
|
|
|
|
全国I.5 |
|
|
|
|
|
全国IV.5 |
|
|
|
|
|
| 双曲线 |
熟练 掌握 |
双曲线的标准方程及其几何性质 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
全国I.5 |
全国I3.5 |
|
|
| |
全国Ⅱ.5 |
全国Ⅱ9.5 |
|
|
|
全国Ⅲ.5 |
全国Ⅲ.5 |
|
|
|
|
广东.5
广东.12 |
|
广东8.5 |
|
|
| |
浙江.4 |
浙江5.5 |
|
|
|
湖南.5 |
湖南.5 |
湖南7.5 |
|
|
|
天津.5 |
天津.5 |
天津2.5 |
|
|
| |
|
陕西7.5 |
|
|
|
福建.5 |
福建.5, |
福建10.5 |
|
|
|
辽宁.5 |
|
辽宁4.5 |
|
|
|
北京春.5 |
北京春.5 |
北京19.14 |
|
|
| |
山东.4 |
山东21.12 |
|
|
| |
|
四川21.12 |
|
|
| |
|
安徽22.14 |
|
|
|
重庆.5 |
重庆.12 |
|
|
|
| |
上海.4 |
|
|
|
| |
江西.4 |
|
|
|
| |
湖北.5 |
|
|
|
|
江苏.5 |
|
|
|
|
|
全国Ⅳ.12 |
|
|
|
|
|
| 抛物线 |
熟练 掌握 |
抛物线的标准方程及其几何性质 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
|
全国I8.5 |
|
|
| |
|
全国Ⅱ21.14 |
|
|
|
全国Ⅲ.4 |
全国Ⅲ.14 |
|
|
|
| |
|
四川9.5 |
|
|
| |
|
江西4.5 |
|
|
| |
|
福建14.4 |
|
|
| |
天津.14 |
|
|
|
| |
山东.14 |
|
|
|
| |
江苏.5 |
|
|
|
|
辽宁.5 |
辽宁.5 |
|
|
|
|
浙江.5 |
|
|
|
|
|
北京春.5 |
|
|
|
|
上海.4
上海春.4 |
|
|
|
|
|
安徽春.4 |
|
|
|
|
|
| 直线与圆锥曲线 |
熟练 掌握 |
综合 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
|
全国I.12 |
全国I.5 |
全国I20.12 |
|
|
|
全国Ⅱ.12 |
|
|
|
|
|
全国Ⅲ.12 |
|
|
|
|
|
辽宁.12 |
|
辽宁10.5 |
|
|
|
上海春.4
上海春.12 |
|
上海11.4 |
|
|
| |
|
山东14.4 |
|
|
|
浙江.12 |
|
浙江19.12 |
|
|
|
天津.4
天津.12 |
|
天津22.14 |
|
|
|
北京春.12 |
北京春.12 |
|
|
|
| |
北京.5 |
|
|
|
|
江苏.12 |
|
|
|
|
|
广东.14 |
|
|
|
|
|
福建.14 |
|
|
|
|
|
湖南.12 |
|
|
|
|
|
重庆.12 |
|
|
|
|
|
安徽春.12 |
|
|
|
|
|
| 轨迹方程 |
熟练 掌握 |
综合 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
北京.14 |
北京4.5 |
|
|
| |
|
湖北7.5 |
|
|
| |
|
四川6.5 |
|
|
| |
广东.14 |
广东18.14 |
|
|
| |
|
江苏17.12 |
|
|
| |
|
陕西21.12 |
|
|
| |
江西.14 |
|
|
|
|
| 综合应用 |
熟练 掌握 |
综合 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| |
全国I.14 |
江西9.5 |
|
|
| |
全国 Ⅱ.14 |
湖南21.14 |
|
|
| |
|
福建20.12 |
|
|
| |
|
重庆22.12 |
|
|
| |
上海.14 |
|
|
|
|
北京.12 |
|
|
|
|
|
三、命题趋势
从上表可以看出,近几年本张考查呈现以下特点:
1、题型和题量:在每年的高考试卷中,选择、填空题2~3题,解答题1道,题目难度兼顾各个层次,即有基
础
题
,又有能力题,本章题目的分值约占全卷的15%。
2、知识点考查:试卷中考查的知识点约占圆锥曲线总知识点的70%,客观题主要考查圆锥曲线的标准方程、几何
性质,解答题往往是以圆锥曲线为主要内容的综合题,问题涉及函数、方程、不等式、三角、平面向量等知识,蕴
含
着数形结合、等价转化、分类讨论等数学思想方法,对学生的数学科能力及一般思维能力的考查要求较高。
3、难度与创新:圆锥曲线的解答题一般出现在倒数第1合创新,因此要得高分,必须在平时练就过硬的准确,迅
速、规范的基本功。
四、复习建议
根据本章知识的重要性以及高考对本章内容的考查情况,复习时应注意以下几个方面:
1、
重点掌握椭圆、双曲线、抛物线的定义和性质,这是因为椭圆、双曲线、抛物线的定义和性质是本章的
基石,高考所考的题目都要涉及到这些内容。
2、重视求曲线的方程或曲线的轨迹,曲线的方程或轨迹问题往往是高考解答题的命题对象,而且难度较
大,所以要求掌握求曲线的方程或曲线的轨迹的一般方法:定义法、直接法、待定系数法、相关点法、参数法
等。
3、加强直线与圆锥曲线的位置关系问题的复习,由于直线与圆锥曲线的位置关系一直为高考的热点,这类
问题常涉及到圆锥曲线的性质和直线的基本知识点、线段的中点、弦长垂直问题,因此分析问题时利用数行结合
思想和设而不求法与弦长公式及韦达定理联系去解决,这样就加强了对数学各种能力的考查。
4、 重视对数学思想、方法进行归纳提炼,以达到优化解题过程的目的。
(1)方程思想,解析几何的题目大部分都以方程形式给定直线和圆锥曲线,因此把直线与椭圆曲线相交的弦
长问题利用韦达定理进行整体处理,就简化了解题运算量。
(2)用好函数思想方法,对与函数曲线上一些动点,在变化过程中会引入一些相互联系、相互制约的量,从
而使一些线的长度及a,b,c,e之间构成函数关系,函数思想在处理这类问题时很有效。
(3)
掌握坐标法,坐标是本章的基本方法,近两年都有考查,因此要加强坐标法的训练。
5、 左翼分析和积累一些圆锥曲线与其他知识点交叉综合的题目,能够通过目标分化以及化归转化的思想和
方法进行剖析和分解,在解决综合问题中去体会和培养自己的逻辑、推理、合理运算以及综合运用知识的能力。
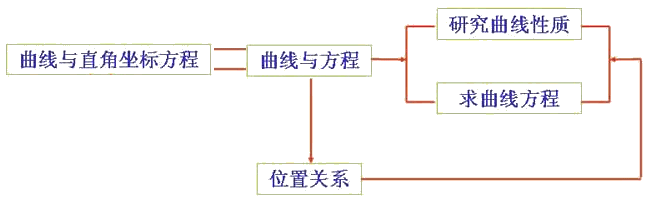
五、思想与方法综览
1、方程思想
通过研究方程的特征或方程与方程之间的关系去研究曲线的性质或曲线与曲线之间的关系,这是解析几何的基本思想之一.处理直线与圆锥曲线问题,一个最为常用的方法是将直线方程代人二次曲线方程,消去一个未知数,变为关于`x(y)`的一元二次方程.此时,应加强韦达定理的运用意识.
[例1]如图,在`△ABC`中,`∠A、∠B、∠C`的对边分别为`a、b、c`,且`b、a、c`成等差数列,`b≥c`已知`B(-1,0),C(1,0)`
(1)求顶点`A`的轨迹`L`;
(2)是否存在直线`m`,使`m`过点`B`并与曲线`L`交于不同的两点`P、Q`,且`|PQ|`恰好等于原点`O`到直线`M`距离的倒数?若存在,求出`m`的方程,若不存在
,说明理由。
解:(1)由题设知
,`b+c=2a`,`|BC|=1-(-1)=2
∴|AB|+|AC|=b+c=2a=2|BC|=4`
又因为`b≥c`,故由椭圆的定义可知,点`A`的轨迹`L`是左半个椭圆(去掉左顶点),
轨迹方程为`x^2/4+y^2/3=1(x≤0且x≠-2)`①
(2)假设存在直线`m`满足题设条件
①当m的斜率存在时,设`m`的方程为`y=k(x+1)`,
把它代入方程①,消去`y`,整理可得`(4k^2+3)x^2十8k^2x十4k^2一12=0`
设`P(x_1,y_1),Q(x_2,y_2)`,则`x_1+x_2=-(8k^2)/(4k^2+3),x_1*x_2=(4k^2一12)/(4k^2+3)`,
又由`x_1≤0,x_2≤0`,即`x_1*x_2≥0`,可得`k^2≥3`
`∴|PQ|=root()((1+k^2)[(x_1+x_2)^2-4x_1x_2])=root()((1+k^2)*[((8k^2)/(4k^2+3))^2-(16(k^2一3))/(4k^2+3)])=(12(k^2+1))/(4k^2+3)`
设原点`O`到直线m的距离为`d`,则`d=|k|/root()(k^2+1)`
`∴|PQ|=1/d`,即`(12(k^2+1))/(4k^2+3)=root()(k^2+1)/|k|`
∴`12|k|(k^2+1)=4k^2+3`,两边平方,整理得`128k^4+120k^2-9=0`
∴`k^2=(-15+-3root()(33))/32`,负值舍去,得`k^2=(3root()(33)-15)/32<3`,这与`k^2≥3`矛盾,表明直线`m`不存在.
②当`m`的斜率不存在时,`m`的方程`x=-1,|PQ|=|y_1-y_2|=3`
而`d=|OB|=1,|PQ|≠1/d`,因而不满足题设条件,所以直线`m`不存在
综合①,②可知,满足题设条件的直线`m`不存在.
点评:本题是一个探索性问题,在求`|PQ|`的过程中,使用了韦达定理,充分利用方程思想解决问题.
2、函数思想
曲线中有很多量与量之间的联系与制约关系,它们之间常构成函数关系,利用函数思想处理这类问题是非常有效
的.
[例2]设椭圆中心在坐标原点,长轴为`x`轴上,离心率`e=root()(3)/2`,已知点`P(0,3/2)`到这个椭圆上的点的最远距离是`root()(7)`,求这个椭圆的方程.
分析:依题意,椭圆方程可设为`x^2/(4b^2)+y^2/b^2=1`,设其上一点`P(x,y)`到点`P`的距离`d`,则`d^2`是关于`y`的二次函数
,且`-b≤y≤b`.
解答:设所求椭圆的直角坐标方程是`x^2/b^2+y^2/b^2=1`.其中`a>b>0`.
由`e^2=c^2/a^2=(a^2-b^2)/a^2=1-(b/a)^2`,可得`b/a=root()(1-e^2)=1/1`,即`a=2b`,
∴得`x^2/(4b^2)+y^2/b^2=1`.
设椭圆上的点`(x,y)`到点`P`之距为`d`,
则`d^2=x^2+(y-3/2)^2=a^2(1-y^2/b^2)^2+y^2-3y+9/4`其中`-b≤y≤b`.
若`b<1/2`,则`y=-b`时,`d^2`(从而`d`)有最大值.
由题设得`(root()(7))^2=(b+3/2)^2`.
由此得`b=root()(7)-3/2>1/2`与`b<1/2` 矛盾.
因此必有`b≥1/2`成立,于是当`y=-1/2`时,`d^2`(从而`d`)有最大值,由题设知`(root()(7))^2=4b^2+3`.由此得`b=1,a=2`.
所有椭圆方程为`x^2/4+y^2=1`.
点评:本题的这种解法是通过建立一个函数关系,使复杂的解几何问题转化为我们熟悉的二次函数给定区间的最值的讨论
,但求值时一定套注意`-b≤y≤b`.
3、分类讨论思想
分类讨论思想是中学数学解题的重要思想,许多问题都涉及分类,一般步骤为:①确定分类的对象和标准;②进行合理的分类;③逐类逐级讨论;④归纳各类结果.
[例3]已知抛物线`y^2=2x`上的点`P(x,y)`,点`A(a,0),a∈R`,设`P`到`A`的距离的最小值为`f(a)`.
(1)求`f(a)`的表达式;
(2)当`1/3≤a≤5`,求`f(a)`的最大值与最小值.
解答:(1)`|PA|^2=(x-a)^2+y^2=[x-(a-1)]^2+2a-1`.
`∵2x=y^2≥0,∴x≥0`. `∴`当`a≥1`时,`a-1≥0`,
`|PA|_min^2=2a-1`(此时`x=a-1`)
`∴f(a)={(|a|,(a<1)),(root()(2a-1),(a>=1)):}`
(2)当`1/3≤a≤5`时,`f(a)={(a,(1/3<=a<1)),(root()(2a-1),(a>=1)):}`
`∵1/3≤a≤1`时,`1/3≤f(a)<1`.
`1≤a≤5`时,`1≤f(a)≤3`.
故`f(a)_min^2=1/3,f(a)_max^2=3`
点评: 一般地,抛物线`y^2=2px`, 则有`d=f(a)={(|a|,(a<=p)),(root()(2ap-p^2),(a>=p^2)):}`
4、参数思想
利用参数法求轨迹方程或利用圆锥曲线的参数形式求解问题,都是参数思想的充分体现.
[例4]已知椭圆`E:x^2/25+y^2/16=1`,点`P(x,y)`是椭圆上一点.
(1)求`x^2+y^2`的最值;
(2)若四边行`ABCD`内接于椭圆`E`,点`A`的横坐标为5,点`C`的纵坐标为4,求四边形`ABCD`的最大面积.
分析:题(1)解题思路比较多.解法一:可从椭圆方程中求出`y^2`代入`x^2+y^2`,转化为`x`的二次函数求解.解法二:用椭圆的参数方程表示椭圆
,将`x,y`代入`x^2+y^2`,转化为三角问题求解.解法三:令`x^2+y^2=r^2`,则利用圆与椭圆有公共点这一条件求`r^2`的最值
,解题时可结合图形思考.
题(2)可将四边形`ABCD`的面积分为两个三角形的面积求解,由于`AC`是定线段
,故长度已定,则当点`B、`点`D`到`AC`所在直线距离最大时,两个三角形的面积最大,此时四边形`ABCD`的面积最大。
解答:(1)解法一:由`x^2/25+y^2/16=1`得`y^2=16(1-x^2/25),x^2+y^2=x^2+16(1-x^2/25)=16+(9x^2)/25,x∈[-5,5]`,由此得`16≤x^2+y^2≤25`,
所以`x^2+y^2`的最大值为25,最小值为16.
解法二:令`x=5costheta,y=4sintheta`,得`x^2+y^2=25cos^2theta+16sin^2theta=16+9cos^2theta∈[16,25]`
所以`x^2+y^2`的最大值为25,最小值为16.
解法三:令`x^2+y^2=r^2`,数形结合可知`x^2+y^2= r^2∈[16,25]`,
所以`x^2+y^2`的最大值为25,最小值为16.
(2)易知`A(5,0),C(0,4)`,如图,设`B`点的坐标为`(5costheta,4sintheta)`.
则直线AC的方程为`x/5+y/4=1`,即`4x+5y-20=0`,点`B`到直线`AC`的距离为`d_1=|20costheta+20sintheta-20|/root()(41)=|20root()(2)sin(theta+pi/4)-20|/root()(41)<=(20root()(2)-20)/root()(41)`
同理可得点`D`到直线`AC`的距离为`d_2=|20costheta+20sintheta-20|/root()(41)=|20root()(2)sin(theta+pi/4)-20|/root()(41)<=(20root()(2)+20)/root()(41)`
∴四边形`ABCD`最大面积`S=1/2|AC|(d_1+d_2)_max=20root()(2)`
5、转化与化归思想
[例5]如图所示,直线`L`的方程为`x=-p/2`,其中`p>0`;椭圆中心`D(2+p/2,0)`,焦点在`x`轴上
,长半轴长为2,短半轴长为1,它的一个顶点为`A(p/2,0)`,问`p`在哪个范围内取值时,椭圆上有四个点不同的点,它们每一个点到点`A`的距离等于该点到直线`L`的距离.
分析:由题意知椭圆的方程为`[x-(2+p/2)]^2/4+y^2=1`,而到点`A`的距离等于到直线`L`的距离的点在以`A`为焦点
,以`L`为准线的抛物线上,因此问题转化为`p`为何值时,椭圆与抛物线有四个不同交点;而讨论两曲线的交点又转化为方程组有解,消元后进一步转化为讨论一个一元方程(一般是一元二次方程)有什么样的解
,并且注意转化过程中应保持等价转化.
解答:依题意知椭圆的方程为`[x-(2+p/2)]^2/4+y^2=1`,以`A`为焦点
,以`L`为准线的抛物线方程为`y^2=2px`.
因此椭圆上有四个点到A的距离等于到L的距离等价与方程组.
`{([x-(2+p/2)]^2/4+y^2=1),(y^2=2px):}`
有四组不同的解.
将②代入①并整理得:`x^2+(7p-4)x+p^2/4+2p=0`
`∵p>0`,∴方程组有四个不同的解等价于方程③的两个不相等的正根(记为`x_1,x_2`),即
`{(Delta=(7p-4)^2-4(p^2/4+2p)>0),(x_1+x_2=-(7p-4)>0),(x_1*x_2=p^2/4+2p):}`
∵`p>0`,∴解该不等式组得`0<p<1/3`.所以所求`p`的范围为`0<p<1/3`
点评:本题将曲线的交点转化为方程组有解,在转化过程中一定要注意转化的等价性
,若在得到方程`x^2+(7p-4)x+P^2/4+2p=0`之后仅仅判定该方程有实根,就不再是等价化了,会导致范围的扩大.
|