应用举例
一、
应用特点
1、抛物线的定义和标准方程;
2、抛物线的几何性质的应用;
3、抛物线的综合应用. 二、案例示范
(回味相关知识与方法,寻找解题办法,若有困难,可以参考“提示”,还有困难,可以参考“解答”或倾听老师的分析示范)
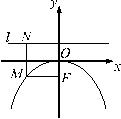
1、求与圆`(x+1)^2+y^2=1`外切且与`y`轴相切的动圆的圆心的轨迹方程。
|
提示 |
示范 |
|
|
根据两圆外切的几何性质,建立等量关系,结合抛物线的定义,从而使问题得以顺利解决,这也是简化解析几何运算的有效途径。 |
解:设动圆圆心为`M(x,y)`,半径为`r`,则动圆圆心到`(-1,0)`的距离是`d=r+1`。
`M`到`x`轴的距离是`r`,则`M`到`x=1`的距离是`d=r+1`,
即动圆圆心为(-1,0)的距离等于它到直线`x=1`的距离,
所以`M`点的轨迹是以为(-1,0)焦点,`x=1`为准线的抛物线。
又圆与`y`轴切于`O`点,所以以圆心在`x`轴上正半轴的圆也满足条件,所以轨迹方程是`y^2=-4x(x<0)`和`y=0(x>0)`
评注:本题主要考查利用抛物线的定义解题,同时对于一些特殊情况不容忽视,否则会产生漏解。 |
2、
已知定点`A(0,t)`,点`M`是抛物线`y^2=x`上一动点,`A`点关于`M`的对称点是`N`。
(1)求`N`点的轨迹方程;
(2)设(1)中所求轨迹与抛物线`y^2=x`交于`B、C`两点,求当`AB_|_AC`时`t`的值。
|
提示 |
示范 |
|
|
求解第(1)问,要抓住`A、N`关于`M`是对称关系;而求`t`的值,要找到`AB_|_AC`的斜率条件,并设法运用这一斜率条件列出关于`t`的方程。 |
解:(1)设`M(x_0,y_0)、N(x,y)`,
则`x_0 =(x+0)/2,y_0=(y+t)/2`。`:.x_0=x/2,y_0=(y+t)/2`适合方程`y^2=x`。
即`(y+t)^2=2x`为所求轨迹方程。
(2)由`{((y+t)^2=2x),(y^2=x):}`,得`y^2-2ty-t^2=0`。
`.:Delta=8t^2>0` ,:.交点存在。设`B(x_1,y_1)、C(x_2,y_2)`,
若`AB_|_AC`,则`k_(AB)xxk_(AC)=1`,即`(y_1-t)/x_1xx(y_2-t)/x_2=-1`。
`:.(y_1-t)(y_2-t)=-y_1^2xxy_2^2`.
由韦达定理得`t^2=2,:.t=+-root()(2)`
评注:
涉及曲线交点问题时,通过解方程组,一般会用上韦达定理,这种问题若直接求根是不明智的解法。 |
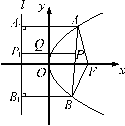
3、在平面指教坐标系`xOy`中,直线`l`与抛物线`y^2=2x`相交于`A、B`两点。
(1)求证:“如果直线过点`T(3,0)`,那么`vec(OA)vec(OB)=3`”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由。
|
提示 |
示范 |
|
|
要证明(1),即证`vec(OA)vec(OB)`=3,而`vec(OA)vec(OB)=x_1x_2+y_1y_2`,所以问题就转化成了直线与圆锥曲线的问题。先假设直线(分`k`存在、不存在在二种情况),然后与`y^2=2x`联立,利用韦达定理求解,对于(1)的逆命题的真假性的判断,可以用举反例方法,也可以又`vec(OA)vec(OB)=3`,得`y_1y_2=-6
或y_1y_2=2`,从而可得直线过(-1,0)或(3,0)点,从而命题是假命题。 |
|
解:(1)证明:设过点`T(3.0)`的直线`l`交抛物线`y^2=2x`于点`A(x_1,y_1)、B(x_2,y_2)`。
当直线`l`的斜率不存在时,直线`l`的方程为`x=3`,此时,直线`l`与抛物线相交与点A(3,`root()(6)`)、B(3,-
`root()(6)` )
`:.``vec(OA)``vec(OB)`=3
当直线`l`的斜率存在时,设直线`l`的方程为`y=k(x-3)`,其中`k!=0`。
由`{(y^2=2x),(y=k(x-3)):}`,得`ky^2-2y-6k=0,:.y_1y_2=-6`。
又`.:x_1=1/2y_1^2,x_2=1/2y_2^2.:.vec(OA)``vec(OB)=x_1x_2+y_1y_2=1/4(y_1y_2)^2+y_1y_2=3`。
综上所述,命题“如果直线l过点`T(3,0)`,那么`vec(OA)``vec(OB)`=3”是真命题。
(2)解析:逆命题是:设直线`l`交抛物线`y^2=2x`与`A、B`两点,如果`vec(OA)``vec(OB)`=3,那么该直线过点`T(3,0)`,该命题是假命题。例如:取抛物线上的点`A(2,2)、B(1/2,1)`,此时`vec(OA)``vec(OB)`=3,直线`AB`的方程为:`y=2/3(x+1)`,而`T(3,0)`不在直线AB上。
说明:由抛物线`y^2=2x`的点`A(x_1,y_1)、B(x_2,y_2)`满足`vec(OA)``vec(OB)`=3,可得`y_1y_2=-6`或`y_1y_2=2`如果`y_1y_2=-6`,可证得直线`AB`过点(3,0);如果`y_1y_2=2`,可证得直线`AB`过点(-1,0),而不过点(3,0)。
评注:无论题目问题多么新颖,都可以转化为我们所熟悉的类型,所以,对于
圆锥曲线的基本题型,基本解法一定要理解透,掌握好。 |
|