|
一、复习目标 掌握椭圆的定义、标准方程和椭圆的简单几何性质,理解椭圆的参数方程。 二、重点难点 三、特别提示 |
| 知识梳理 1、椭圆的定义 第一定义:平面内与两个定点`F_1、F_2`的距离的和等于常数(大于`|F_1F_2|`)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距. 第二定义:平面内到定点`F(c,0)`的距离与到直线`l:x=a^2/c`的距离之比是常数`c/a(0<c<a)`的动点的轨迹叫做椭圆. 注意:(1)定义1中,“定值大于`|F_1F_2|`”(即`2a>2c`)是必要条件,当`2a=2c`时,动点轨迹是两焦点的连线段;而当`2a<2c`时,动点轨迹不存在. (2)定义2中,定点`F`是椭圆的焦点,定直线`l`是椭圆的相应于焦点`F`的准线. 2、椭圆的标准方程与几何性质
3、椭圆的参数方程 |
|
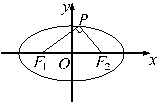
应用举例 一、 应用特点 1、椭圆的定义及应用; 2、椭圆的几何性质及应用; 3、椭圆基本量的讨论. 二、案例示范 1、设`F_1`、`F_2`是椭圆`x^2/9+y^2/4=1`的两个焦点,P为椭圆上一点,已知P、`F_1`、`F_2`是一个直角三角形的顶点,且|`PF_1`|>|`PF_2`|, 求`|PF_1|/|PF_2|`的值。
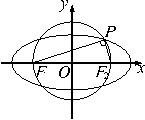
2、如下图,在直角坐标系`xOy`中,设椭圆`C:x^2/a^2+y^2/b^2=1(a>b>0)`的左右两个焦点分别为`F_1、F_2 `,过右焦点`F_2`且与`x`轴垂直的直线 `l`与椭圆`C`相交,其中一个交点为`M(root()(2),1)`。求椭圆`C`的方程。
3、 已知椭圆`C:x^2/a^2+y^2/b^2=1(a>b>0)`的长轴端点为`A、B`,若椭圆`C`上存在点`Q`,使`/_AQB=120^ 。`,求椭圆`C`的离心率`e`的取值范围。
|
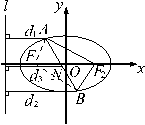
| 实践体验 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高) 1、已知`A、B`是椭圆`x^2/a^2+y^2/(9/25a^2)`上的点,`F_2`是右焦点且`|AF_2|+|BF_2|=8/5a`,`AB`的中点`N`到左准线的距离等于`3/2`,求此椭圆方程.
2、 设椭圆`x^2/a^2+y^2/b^2=1(a>b>0)`的两焦点为`F_1、F_2`,若在椭圆上存在一点P,使`vec(PF_1)`•`vec(PF_2)`=`0`,求椭圆的离心率`e`的取值范围.
|
| 拓展探究 1、如图,在直角梯形`ABCD`中,`AD=3,AB=4,BC=root()(3)`, 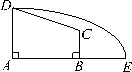 曲线`DE`上任意一点到A、B两点距离之和都相等. 曲线`DE`上任意一点到A、B两点距离之和都相等.(1)适当建立坐标系,求曲线DE的方程. (2)过`C`点能否作一条直线与曲线`DE`相交且以`C`为中点弦?如果不能,请说明理由;如果能,请求出弦所在的直线方程.
|
|
|
|
|
学习感悟 |
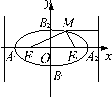
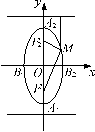
 F_2|)=4a-8/5a=12/5a`.
F_2|)=4a-8/5a=12/5a`.