2004年

解答题

17．（本小题满分12分）

已知四棱锥P—ABCD，底面ABCD是菱形，平面ABCD，PD=AD，　

点E为AB中点，点F为PD中点.

   （1）证明平面PED⊥平面PAB；

   （2）求二面角P—AB—F的平面角的余弦值.

            解答

18．（本小题满分12分）

设全集U=R

（1）解关于x的不等式

       
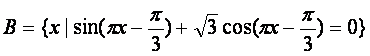        若（  _∪A）∩B恰有3个元素，求a的取值范围.

      解答

19．（本小题满分12分）

设椭圆方程为，过点M（0，1）的直线l交椭圆于点A、B，O是坐标原点，

点P满足，点N的坐标为，当l绕点M旋转时，求：

   （1）动点P的轨迹方程；

   （2）的最小值与最大值.

解答

20．（本小题满分12分）

甲方是一农场，乙方是一工厂. 由于乙方生产须占用甲方的资源，因此

甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付

甲方的情况下，乙方的年利润x（元）与年产量t（吨）满足函数关系

.若乙方每生产一吨产品必须赔付甲方s元（以下称s为赔付价格），

   （1）将乙方的年利润w（元）表示为年产量t（吨）的函数，并求出乙方

获得最大利润的年产量；

   （2）甲方每年受乙方生产影响的经济损失金额（元），在乙方

按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，

应向乙方要求的赔付价格s是多少？

解答

21．（本小题满分14分）

已知函数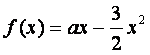的最大值不大于，又当

   （1）求a的值；

   （2）设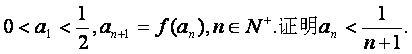

 解答

22．（本小题满分12分）

已知函数.

   （1）求函数的反函数的导数

   （2）假设对任意成立，求实

数m的取值范围.

解答

2005年

解答题

     17．（本小题满分12分）

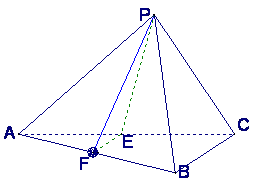
 已知三棱锥P—ABC中，E、F分别是AC、AB的中点,△ABC，△PEF都是正三角形，PF⊥AB.

    （Ⅰ）证明PC⊥平面PAB；

    （Ⅱ）求二面角P—AB—C的平面角的余弦值；

    （Ⅲ）若点P、A、B、C在一个表面积为12π的

         球面上，求△ABC的边长.

解答

18．（本小题满分12分）

     如图，在直径为1的圆O中，作一关于圆心对称、

     邻边互相垂直的十字形，其中

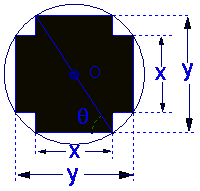
    （Ⅰ）将十字形的面积表示为的函数；

    （Ⅱ）为何值时，十字形的面积最大？最大面积是多少？

解答

19．（本小题满分12分）

  已知函数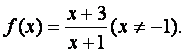设数列}满足，数列}满足

    （Ⅰ）用数学归纳法证明；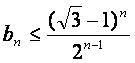

    （Ⅱ）证明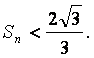

解答

 20．（本小题满分12分）

 某工厂生产甲、乙两种产品，每种产品都是经过第一和第二工序加工而成，

 两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级.对

 每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品.

   （Ⅰ）已知甲、乙两种产品每一道工序的加工结

         果为A级的概率如表一所示，分别求生产

         出的甲、乙产品为一等品的概率P甲、P乙；

   （Ⅱ）已知一件产品的利润如表二所示，用ξ、

         η分别表示一件甲、乙产品的利润，在

        （I）的条件下，求ξ、η的分布列及

Eξ、Eη；

   （Ⅲ）已知生产一件产品需用的工人数和资金额

         如表三所示.该工厂有工人40名，可用资

         品的数量，在（II）的条件下，x、y为何

         值时，最大？最大值是多少？

        （解答时须给出图示）                    

     解答

21．（本小题满分14分）

已知椭圆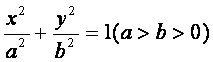的左、右焦点分别是F1（－c，0）、F2（c，0），

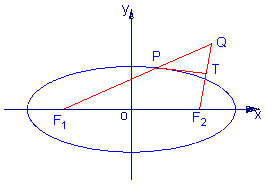
Q是椭圆外的动点，满足点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，

并且满足

   （Ⅰ）设为点P的横坐标，证明；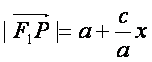

   （Ⅱ）求点T的轨迹C的方程；

   （Ⅲ）试问：在点T的轨迹C上，是否存在点M，

         使△F1MF2的面积S=若存在，求∠F1MF2

         的正切值；若不存在，请说明理由.

解答

22．（本小题满分12分）

 函数在区间（0，+∞）内可导，导函数是减函数，且 设

是曲线在点（）得的切线方程，并设

函数

   （Ⅰ）用、、表示m；

   （Ⅱ）证明：当；

   （Ⅲ）若关于的不等式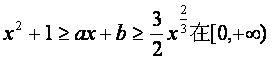上恒成立，其中a、b为实数，

         求b的取值范围及a与b所满足的关系.

     解答

    2006

解答题

(17) (本小题满分12分)

已知函数，.求:

(I) 函数的最大值及取得最大值的自变量的集合；

(II) 函数的单调增区间.

解答

18．（本小题满分12分）

甲、乙两班各派2名同学参加年级数学竞赛，参赛同学成绩及格的概率都为0.6，

且参赛同学的成绩相互之间没有影响，求：

（1）甲、乙两班参赛同学中各有1名同学成绩及格的概率；

（2）甲、乙两班参赛同学中至少有1名同学成绩及格的概率．

解答

19．（本小题满分12分）

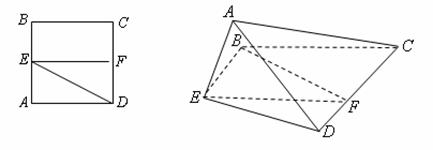
已知正方形，分别是边的中点，将沿折起，

如图所示，记二面角的大小为（）．

（1）证明平面；

（2）若为正三角形，试判断点在平面内的射影是否在直线

上，证明你的结论，并求角的余弦值.

解答

20．（本小题满分12分）

已知等差数列的前项和为，．

（1）求的值；

（2）若与的等差中项为，满足，求数列的前项和．

 解答

21．（本小题满分12分）

已知函数，，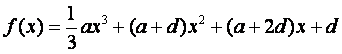

其中，设为的极小值点，为的极值点，，

并且，将点依次记为．

（1）求的值；

（2）若四边形为梯形且面积为1，求的值．

解答

22．（本小题满分14分）

已知点是抛物线上的两个动点，是坐标原点，

向量满足，设圆的方程为．

（1）证明线段是圆的直径；

（2）当圆的圆心到直线的距离的最小值为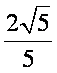时，求的值．

解答

2007年

解答题

17．（本小题满分12分）

某公司在过去几年内使用某种型号的灯管1000支，该公司对这些灯管的使用寿命

（单位：小时）进行了统计，统计结果如下表所示：

（I）将各组的频率填入表中；

（II）根据上述统计结果，计算灯管使用寿命不足1500小时的频率；

（III）该公司某办公室新安装了这种型号的灯管3支，若将上述频率作为概率，

试求至少有2支灯管的使用寿命不足1500小时的概率．

解答

18．（本小题满分12分）

如图，在直三棱柱中，，，分别为棱的中点，

为棱上的点，二面角为．

（I）证明：；

（II）求的长，并求点到平面的距离．

解答

19．（本小题满分12分）

已知函数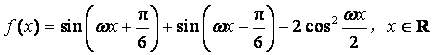（其中）

（I）求函数的值域；

（II）若函数的图象与直线的两个相邻交点间的距离为，

求函数的单调增区间．

解答

20．（本小题满分12分）

已知数列，满足，，且（）

（I）令，求数列的通项公式；

（II）求数列的通项公式及前项和公式．

解答

21．（本小题满分14分）

已知正三角形的三个顶点都在抛物线上，其中为坐标原点，

设圆是的内接圆（点为圆心）

（I）求圆的方程；

（II）设圆的方程为，过圆上任意一点分别

作圆的两条切线，切点为，求的最大值和最小值．

解答

22．（本小题满分12分）

已知函数，，且对任意的实数均

有，．

（I）求函数的解析式；

（II）若对任意的，恒有，求的取值范围．

解答