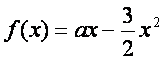 的最大值不大于
的最大值不大于
21.(本小题满分14分)
已知函数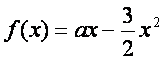 的最大值不大于
的最大值不大于![]() ,又当
,又当
(1)求a的值;
(2)设
本小题主要考查函数和不等式的概念,考查数学归纳法,以及灵活运用
数学方法分析和解决问题的能力. 满分14分.
(1)解:由于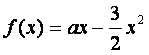 的最大值不大于
的最大值不大于![]() 所以
所以
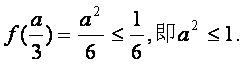 ①
………………3分
①
………………3分
又![]() 所以
所以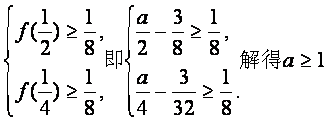 .
②
.
②
由①②得![]() ………………6分
………………6分
(2)证法一:(i)当n=1时,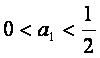 ,不等式
,不等式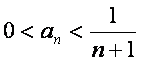 成立;
成立;
因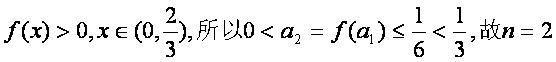 时不等式也成立.
时不等式也成立.
(ii)假设![]() 时,不等式
时,不等式![]() 成立,因为
成立,因为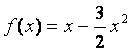 的
的
对称轴为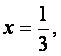 知
知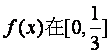 为增函数,所以由
为增函数,所以由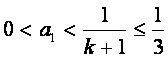 得
得
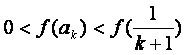 ………………8分
………………8分
于是有
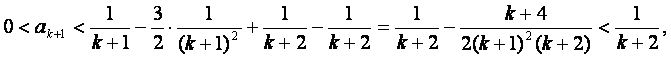
…………12分
所以当n=k+1时,不等式也成立.
根据(i)(ii)可知,对任何![]() ,不等式
,不等式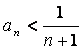 成立.……14分
成立.……14分
证法二:(i)当n=1时,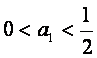 ,不等式
,不等式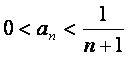 成立;
成立;
(ii)假设![]() 时不等式成立,即
时不等式成立,即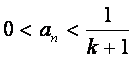 ,则当n=k+1时,
,则当n=k+1时,
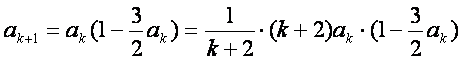 ………………8分
………………8分
因 所以
所以
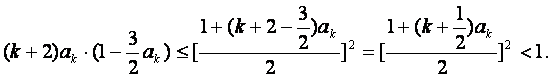 ……12分
……12分
于是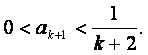 因此当n=k+1时,不等式也成立.
因此当n=k+1时,不等式也成立.
根据(i)(ii)可知,对任何![]() ,不等式
,不等式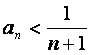 成立.…………14分
成立.…………14分
证法三:(i)当n=1时,![]() 不等式
不等式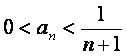 成立;
成立;
(ii)假设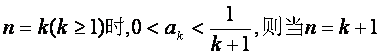 时.
时.
若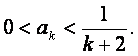 则
则 ①…………8分
①…………8分
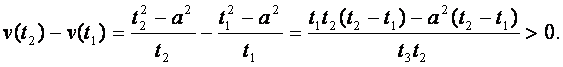
所以![]() 都是增函数.
都是增函数.
因此当![]() 时,
时,![]() 的最大值为
的最大值为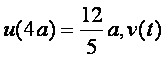 的最小值为
的最小值为
 而不等式②成立当且仅当
而不等式②成立当且仅当![]() 即
即
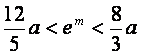 ,于是得
,于是得
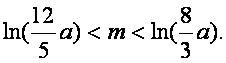 ………………12分
………………12分
解法二:由![]() 得
得
![]()
设![]()
于是原不等式对于![]() 恒成立等价于
恒成立等价于![]() ③…7分
③…7分
由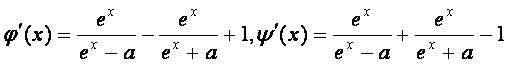 ,注意到
,注意到
![]() 故有
故有![]() ,从而可
,从而可![]() 均在
均在
![]() 上单调递增,因此不等式③成立当且仅当
上单调递增,因此不等式③成立当且仅当
![]() 即
即
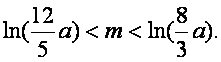 ………………12分
………………12分
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。