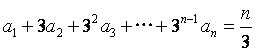 ,
,三、解答题
(17)(本小题满分12分)
设数列![]() 满足
满足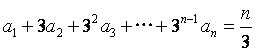 ,
,![]() .
.
(Ⅰ)求数列![]() 的通项;
的通项;
(Ⅱ)设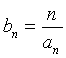 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(18)(本小题满分12分)
设![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量![]() 表示方程
表示方程![]()
实根的个数(重根按一个计).
(Ⅰ)求方程![]() 有实根的概率;
有实根的概率;
(Ⅱ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程![]() 有实根的概率.
有实根的概率.
(19)(本小题满分12分)
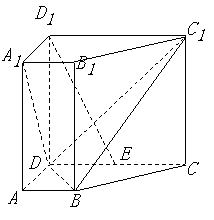 如图,在直四棱柱
如图,在直四棱柱![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)设![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(20)(本小题满分12分)
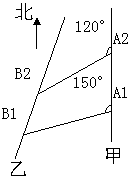 如图,甲船以每小时
如图,甲船以每小时![]() 海里的速度向正北方航行,乙船按固定方向匀速直线
海里的速度向正北方航行,乙船按固定方向匀速直线
航行,当甲船位于![]() 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西![]() 方向的
方向的![]() 处,此时两船
处,此时两船
相距![]() 海里,当甲船航行
海里,当甲船航行![]() 分钟到达
分钟到达![]() 处时,
处时,
乙船航行到甲船的北偏西![]() 方向
方向
的![]() 处,此时两船相距
处,此时两船相距![]() 海里,
海里,
问乙船每小时航行多少海里?
(21)(本小题满分12分)
已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 上的点到焦点距离的
上的点到焦点距离的
最大值为![]() ,最小值为
,最小值为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点(
两点(![]() 不是左右顶点),
不是左右顶点),
且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的右顶点,求证:直线
的右顶点,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
(22)(本小题满分14分)
设函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,判断函数
时,判断函数![]() 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)求函数![]() 的极值点;
的极值点;
(Ⅲ)证明对任意的正整数![]() ,不等式
,不等式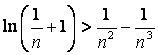 都成立.
都成立.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。