解答题

全国卷Ⅰ(文)

21．（本小题满分12分）

设是一常数，过点的直线与抛物线交于相异

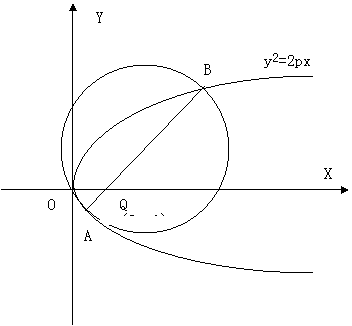
两点A、B，以线段AB为直经作圆H（H为圆心）。试证抛物线顶点

在圆H的圆周上；并求圆H的面积最小时直线AB的方程。

 解答

全国卷Ⅱ(文)

21．（本小题满分12分）

       若函数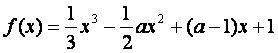在区间（1，4）内为减函数，在区间

（6，+∞）上为增函数，试求实数a的取值范围.

解答 

全国卷Ⅲ(文)

21．（本小题满分12分）三棱锥P-ABC中，侧面PAC与底面ABC垂直，PA=PB=PC=3，

（1）求证：AB ⊥ BC； 

（2）设AB=BC=，求AC与平面PBC所成角的大小.　

解答

全国卷Ⅳ(文)

21．（本小题满分12分）

   如图，四棱锥P—ABCD中，底面ABCD 为矩形，AB=8，AD=4，

侧面PAD为等边三角形，并且与底面所成二面角为60°.

（Ⅰ）求四棱锥P—ABCD的体积；

（Ⅱ）证明PA⊥BD.

解答

天津卷(文)

21.（本小题满分12分）

已知函数是R上的奇函数，当时取得极值。

（1）求的单调区间和极大值；

（2）证明对任意，，不等式恒成立。

解答

辽宁卷

21．（本小题满分14分）

已知函数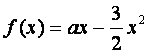的最大值不大于，又当

   （1）求a的值；

   （2）设

 解答

江苏卷

21.已知椭圆的中心在原点，离心率为  EQ \F(1,2) ，一个焦点是F（-m,0）

(m是大于0的常数).    

(Ⅰ)求椭圆的方程；

   (Ⅱ)设Q是椭圆上的一点，且过点F、Q的直线与y轴交于点M. 若，

求直线的斜率.

 解答

浙江卷(文)

（21）（本题满分12分）

已知a为实数，

（Ⅰ）求导数；

（Ⅱ）若，求在[--2，2] 上的最大值和最小值；

（Ⅲ）若在（--∞，--2]和[2，+∞）上都是递增的，求a的取值范围。

解答

福建卷(文)

21．（本小题满分12分）

如图，P是抛物线C：y=x²上一点，直线l过点P并与抛物线C在

点P的切线垂直，l与抛物线C相交于另一点Q.

（Ⅰ）当点P的横坐标为2时，求直线l的方程；

（Ⅱ）当点P在抛物线C上移动时，求线段PQ中点M的轨迹方程，

并求点M到x轴的最短距离.

            解答

湖北卷(文)

21．（本小题满分12分）

为防止某突发事件发生，有甲、乙、丙、丁四种相互独立的预防措施

可供采用，单独采用甲、乙、丙、丁预防措施后此突发事件不发生的

概率（记为P）和所需费用如下表：

预防方案可单独采用一种预防措施或联合采用几种预防措施，在总费用不超

过120万元的前提下，请确定一个预防方案，使得此突发事件不发生的概率最大.

 解答

湖南卷(文)

21．（本小题满分12分）

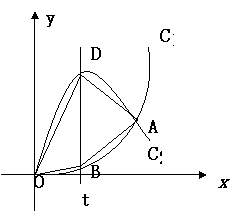
如图，已知曲线C₁：y=x³(x≥0)与曲线C₂:y=－2x³+3x(x≥0)交于O，A,

直线x=t(0<t<1)与曲线C₁,C₂分别交于B，D.

（Ⅰ）写出四边形ABOD的面积S与t的函数关系式S=f(t);

（Ⅱ）讨论f(t)的单调性，并求f(t) 的最大值.

                         解答

重庆卷(文)

21．（本小题满分12分）

设是一常数，过点的直线与抛物线交于相异

两点A、B，以线段AB为直经作圆H（H为圆心）。试证抛物线顶点

在圆H的圆周上；并求圆H的面积最小时直线AB的方程。

北京卷(文)

（19）（本小题满分12分）

    某段城铁线路上依次有A、B、C三站，AB=15km，BC=3km，在列车运行

时刻表上，规定列车8时整从A站发车，8时07分到达B站并停车1分钟，8时

12分到达C站，在实际运行中，假设列车从A站正点发车，在B站停留1分钟，

并在行驶时以同一速度匀速行驶，列车从A站到达某站的时间与时刻表

上相应时间之 差的绝对值称为列车在该站的运行误差。

    （I）分别写出列车在B、C两站的运行误差

    （II）若要求列车在B，C两站的运行误差之和不超过2分钟，求的取值范围

     解答

上海卷(文)

21、(本题满分16分) 第1小题满分4分, 第2小题满分6分, 第3小题满分6分

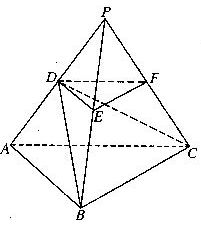  如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上

的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.

(棱长和是指多面体中所有棱的长度之和)

(1)     证明：P-ABC为正四面体；

(2)     若PD=PA, 求二面角D-BC-A的

大小；(结果用反三角函数值表示)

(3)     设棱台DEF-ABC的体积为V, 是

否存在体积为V且各棱长均相等的直

平行六面体,使得它与棱台DEF-ABC

有相同的棱长和? 若存在,请具体构造

出这样的一个直平行六面体,并给出证

明；若不存在,请说明理由.

  解答

广东卷

21. (12分)设函数   其中常数m为整数.

 (1) 当m为何值时,

 (2) 定理: 若函数g(x) 在[a, b ]上连续,且g(a) 与g(b)异号,则至少

存在一点x₀∈(a,b),使g(x₀)=0.

 试用上述定理证明:当整数m>1时,方程f(x)= 0,

在[e^-ｍ-m ,e^2ｍ-m ]内有两个实根.

  解答