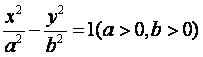 的右焦点为F,若过点F且倾斜角
的右焦点为F,若过点F且倾斜角福建(理)
一、选择题(每题5分)
(10)已知双曲线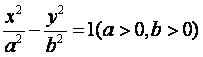 的右焦点为F,若过点F且倾斜角
的右焦点为F,若过点F且倾斜角
为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率
的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11)已知![]() 点C在
点C在![]() =30°。
=30°。
设![]() ,则
,则![]() 等于(
)
等于(
)
(A)![]() (B)3 (C)
(B)3 (C)![]() (D)
(D)![]()
(12)对于直角坐标平面内的任意两点![]() ,定义它们之间的一种
,定义它们之间的一种
“距离”:
![]()
给出下列三个命题:
①若点C在线段AB上,则![]()
②在![]() 中,若
中,若![]() 则
则![]()
③在![]() 中,
中,![]()
其中真命题的个数为( )
(A)0 (B)1 (C)2 (D)3
二、填空题(每题4分)
(14)已知直线![]() 与抛物线
与抛物线![]() 相切,则a=
相切,则a=
(16)如图,连结![]() 的各边中点得到一个新的
的各边中点得到一个新的![]() 又连结
又连结![]() 的各边中点
的各边中点
得到![]() ,如此无限继续下去,得到一系列三角形:
,如此无限继续下去,得到一系列三角形:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
这一系列三角形趋向于一个点M。已知![]()
![]() 则点M的坐标是____。
则点M的坐标是____。
三、解答题
(20)(本小题满分12分)
已知椭圆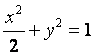 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(I)求过点O、F,并且与椭圆的左准线![]() 相切的圆的方程;
相切的圆的方程;
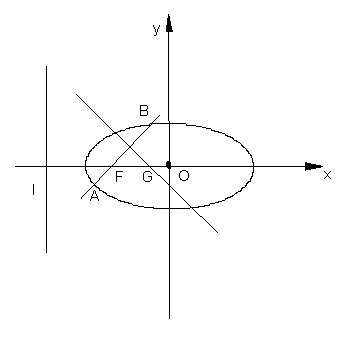
(II)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分
线与![]() 轴交于点G,求点G横坐标的取值范围。
轴交于点G,求点G横坐标的取值范围。
浙江(理)
一、选择题(每小题5分)
(5)若双曲线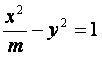 上的点到左准线的距离是到左焦点距离的
上的点到左准线的距离是到左焦点距离的![]() ,则m=()
,则m=()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
三、解答题
(19)如图,椭圆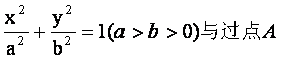 (2,0)、B(0,1)
(2,0)、B(0,1)
的直线有且只有一个公共点T,且椭圆的离心率e=![]() 。
。
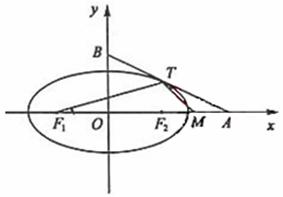
(Ⅰ)求椭圆方程;
(Ⅱ)设F1、F2分别为椭圆的左、右焦点,M为线段AF2的中点,
求证:∠ATM=∠AF1T。
天津(理)
一、选择题(每小题5分)
(2)如果双曲线的两个焦点分别为F1(-3,0)、F2(3,0),一条渐近线方程
为y=![]() x,那么它的两条准线间的距离是()
x,那么它的两条准线间的距离是()
(A)6![]() (B)4 (C)2 (D)1
(B)4 (C)2 (D)1
二、填空题(每小题4分)
(14)设直线ax-y+3=0与圆(x-1)2+(y-2)2=4相交于A、B两点,
且弦AB的长为2![]() ,则a=_______.解答
,则a=_______.解答
三、解答题
(22)(本小题满分14分)
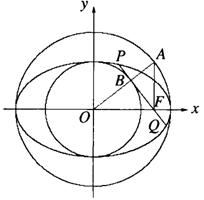
如图,以椭圆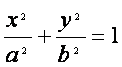 (a>b>0)的中心O为圆心,分别以a和b为
(a>b>0)的中心O为圆心,分别以a和b为
半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大
圆于第一象限内的点A.连结OA交小圆于点B.设直线BF是小圆的切线.
(Ⅰ)证明c2=ab,并求直线BF与y轴的交点M的坐标;
(Ⅱ)设直线BF交椭圆于P、Q两点,证明![]() ·
·![]() =
=![]() b2.
b2.
江苏
一、选择题(每小题5分)
(2)圆![]() 的切线方程中有一个是()
的切线方程中有一个是()
(A)x-y=0 (B)x+y=0 (C)x=0 (D)y=0
(6)已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,
满足![]() =0,则动点P(x,y)的轨迹方程为()
=0,则动点P(x,y)的轨迹方程为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
三、解答题
(17)(本小题满分12分,第一小问满分5分,第二小问满分7分)
已知三点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0).
(6,0).
(Ⅰ)求以![]() 、
、![]() 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点P、![]() 、
、![]() 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为![]() 、
、![]() 、
、![]() ,
,
求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的双曲线的标准方程。
的双曲线的标准方程。
(19)(本小题满分14分,第一小问满分4分,第二小问满分5分,
第三小问满分5分)
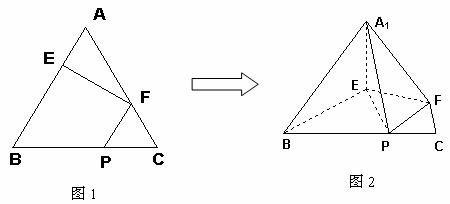
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足
AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到![]() 的位置,
的位置,
使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示)
辽宁(理)
一、选择题(每题5分)
(4)
双曲线![]() 的两条渐近线与直线
的两条渐近线与直线![]() 围成一个三角形区域,表示该
围成一个三角形区域,表示该
区域的不等式组是( )
(A) (B)
(B)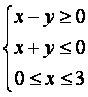 (C)
(C)
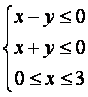 (D)
(D)
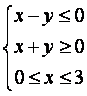
(6)![]() 的三内角
的三内角![]() 所对边的长分别为
所对边的长分别为![]() 设向量
设向量![]() ,
,
![]() ,
若
,
若![]() ,则角
,则角![]() 的大小为(
)
的大小为(
)
(A)![]() (B)
(B)![]() (C)
(C)
![]() (D)
(D)
![]()
(7)
与方程![]() 的曲线关于直线
的曲线关于直线![]() 对称的曲线的方程为(
)
对称的曲线的方程为(
)
(A)![]() (B)
(B)
![]()
(C)
![]() (D)
(D)
![]()
(8)
曲线 与曲线
与曲线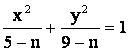 (5<n<9)的(
)
(5<n<9)的(
)
(A)焦距相等 (B) 离心率相等 (C)焦点相同 (D)准线相同
(10)
直线![]() 与曲线
与曲线![]()
![]() 的公共点的个
的公共点的个
数为( )
(A)1 (B)2 (C)3 (D)4
(12)
设![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,![]() ,
,
若![]() ,则实数
,则实数![]() 的取值范围是(
)
的取值范围是(
)
(A)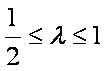 (B)
(B)
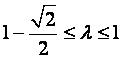
(C)
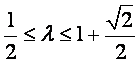 (D)
(D)
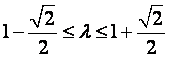
(20) (本小题满分14分)
已知点![]() ,
,![]()
![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐
是坐
标原点,向量![]() ,
,![]() 满足
满足![]() .设圆
.设圆![]() 的方程为
的方程为
![]()
(I)
证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(II)当圆C的圆心到直线X-2Y=0的距离的最小值为时,求P的值。
重庆(理)
一、选择题(每小题5分)
(3)过坐标原点且与圆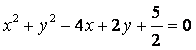 相切的直线的方程为()
相切的直线的方程为()
(A)![]() 或
或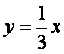 (B)
(B)![]() 或
或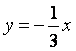
(C)![]() 或
或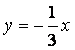 (D)
(D)![]() 或
或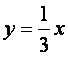
(4)对于任意的直线![]() 与平面
与平面![]() ,在平面
,在平面![]() 内必有直线
内必有直线![]() ,是
,是![]() 与
与![]()
(A)平行 (B)相交 (C)垂直 (D)互为异面直线
三、解答题
(22)(本小题满分12分)
已知一列椭圆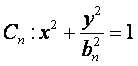 ,
,![]() 若椭圆
若椭圆![]() 上有一点
上有一点![]() ,
,
使![]() 到右准线
到右准线![]() 的距离
的距离![]() 是
是![]() 与
与![]() 的等差中项,
的等差中项,
其中![]() 分别是
分别是![]() 的左、右焦点。
的左、右焦点。

(Ⅰ)试证: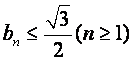 ;
;
(Ⅱ)取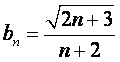 ,并用
,并用![]() 表示
表示![]() 的面积,
的面积,
试证:![]() 且
且![]()
湖南(理)
一、选择题(每题5分)
7.过双曲线M:x2-![]() =1的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐
=1的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐
近线分别相交于点B、C,且|AB|=|BC|,则双曲线M的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若圆x2+y2-4x-4y-10=0上至少有三个不同的点到直线l:ax+by=0的距离为2![]() ,
,
则直线l的倾斜角的取值范围是( )
A.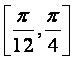 B.
B.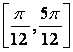 C.
C. 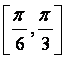 D.
D.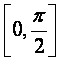
二、填空题(每题4分)
13.曲线y=![]() 和y=x2在它们交点处的两条切线与x轴所围成的三角形的面积是
.
和y=x2在它们交点处的两条切线与x轴所围成的三角形的面积是
.
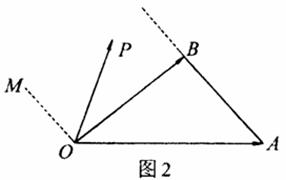
15.如图2,OM∥AB,点P在由射线OM、线段OB及AB的延长线围成的阴影区域
内(不含边界)运动,且![]() ,则x的取值范围是
;当x=-
,则x的取值范围是
;当x=-![]() 时,
时,
y的取值范围是 .
三、解答题
21.(本小题满分14分)
已知椭圆C1: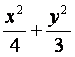 =1,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆
=1,抛物线C2:(y-m)2=2px(p>0),且C1、C2的公共弦AB过椭圆
C1的右焦点.
(Ⅰ)当AB⊥x轴时,求m、p的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)是否存在m、p的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的
m、p的值;若不存在,请说明理由.
湖北(理)
一、选择题(每题5分)
1.已知向量![]() 是不平行于x轴的单位向量,且
是不平行于x轴的单位向量,且![]() ,则b=(
)
,则b=(
)
A. B.
B. C..
C.. D.(1,0)
D.(1,0)
7.设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A、B两点,
点Q与点P关于y轴对称,O为坐标原点,若![]() ,则P点
,则P点
的轨迹方程是( )
A. B.
B.
![]()
C.![]() D.
D.
![]()
二、填空题(每题5分)
13.已知直线![]() 与圆x2-2x+y2=0相切,则a的值为________。
与圆x2-2x+y2=0相切,则a的值为________。
三、解答题
20.(本小题满分14分)
设A、B分别为椭圆 (a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
(a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
且x=4为它的右准线。
(Ⅰ)求椭圆的方程;
(Ⅱ)设P为右准线上不同于点(4,0)的任意一点,若直线AP、BP分别与椭圆相交于
异于A、B的点M、N,证明点B在以MN为直径的圆内。
(此题不要求在答题卡上画图)
广东
一、选择题(每题5分)
5.给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,
那么这条直线和交线平行。
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直
于这个平面。
③如果两条直线都平行于一个平面,那么这两条直线相互平行。
④如果一个平面经过另一个平面的一条垂线,那么这两个平面相互垂直。
其中真命题的个数是()
A.4 B.3 C.2 D.1
8.已知双曲线3x2+y2=9,则双曲线右支上的点P到右焦点的距离与点P到
右准线的距离之比等于()
A.![]() B.
B.![]() C.2
D.4
C.2
D.4
北京(理)
一、选择题(每题5分)
(2)若a与b-c都是非零向量,则“a·b=a·c”是“a⊥(b-c)”的 ( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(4)平面α的斜线AB交α于点B,过定点A的动直线l与AB垂直,且交α于点C,
则动点C的轨迹是( )
(A)一条直线 (B)一个圆
(C)一个椭圆 (D)双曲线的一支
二、填空题(每题5分)
(11)若三点A(2,2),B(a,0),C(0,b)(ab≠0)共线,则 的值等于____.
的值等于____.
(13)已知点P(x,y)的坐标满足条件 点O为坐标原点,那么,|PO|的
点O为坐标原点,那么,|PO|的
最小值等于___________,最大值等于________.
三、解答题
(19)(本小题共14分)
已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2![]() .记动点P的
.记动点P的
轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)若A,B是W上的不同两点,O是坐标原点,求![]() 的最小值.
的最小值.
上海(理)
一、填空题(每小题4分)
2.已知圆![]() -4
-4![]() -4+
-4+![]() =0的圆心是点P,则点P到直线
=0的圆心是点P,则点P到直线![]() -
-![]() -1=0的
-1=0的
距离是 .解答
7.已知椭圆中心在原点,一个焦点为F(-2![]() ,0),且长轴长是短轴长
,0),且长轴长是短轴长
的2倍,则该椭圆的标准方程是 .解答
8.在极坐标系中,O是极点,设点A(4,![]() ),B(5,-
),B(5,-![]() ),
),
则△OAB的面积是 .解答
11.若曲线![]() =|
=|![]() |+1与直线
|+1与直线![]() =
=![]() +
+![]() 没有公共点,则
没有公共点,则![]() 、
、![]() 分别应满足
分别应满足
的条件是 .解答
二、选择题(每小题4分)
 13.如图,在平行四边形ABCD中,下列结论中错误的是(
)
13.如图,在平行四边形ABCD中,下列结论中错误的是(
)
(A)![]() =
=![]() ;(B)
;(B)![]() +
+![]() =
=![]() ;
;
(C)![]() -
-![]() =
=![]() ;(D)
;(D)![]() +
+![]() =
=![]() .
.
16.如图,平面中两条直线![]() 和
和![]() 相交于点O,对于平面上任意一点M,
相交于点O,对于平面上任意一点M,
若![]() 、
、![]() 分别是M到直线
分别是M到直线![]() 和
和![]() 的距离,则称有序非负实数对(
的距离,则称有序非负实数对(![]() ,
,![]() )是
)是
点M的“距离坐标”.已知常数![]() ≥0,
≥0,![]() ≥0,给出下列三个命题:
≥0,给出下列三个命题:

①若![]() =
=![]() =0,则“距离坐标”为(0,0)的点有且仅有1个;
=0,则“距离坐标”为(0,0)的点有且仅有1个;
②若![]() =0,且
=0,且![]() +
+![]() ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(![]() ,
,![]() )的点有且仅有2个;
)的点有且仅有2个;
③若![]() ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(![]() ,
,![]() )的点有且仅有4个.
)的点有且仅有4个.
上述命题中,正确命题的个数是 ( )
(A)0; (B)1; (C)2; (D)3.
三、解答题
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分)
在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]()
![]() =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
山东(理)
一、选择题(每小题5分)
7.在给定椭圆中,过焦点且垂直于长轴的弦长为![]() ,焦点到相应准线的
,焦点到相应准线的
距离为1,则该椭圆的离心率为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题(每小题4分)
14.已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1)、
B(x2,y2)两点,则y21+y22的最小值是________. 解答
三、解答题
21.(本小题满分12分)
双曲线C与椭圆 有相同的焦点,直线y=
有相同的焦点,直线y=![]() x为C的一条渐近线.
x为C的一条渐近线.
(Ⅰ)求双曲线C的方程;
(Ⅱ)过点P(0,4)的直线l,交双曲线C于A、B两点,交x轴于Q点
(Q点与C的顶点不重合).当![]() =λ1
=λ1![]() =λ2
=λ2![]() ,且λ1+λ2=
,且λ1+λ2=![]() 时,求Q点的坐标.
时,求Q点的坐标.
江西(理)
一、选择提(每题5分)
4.设O为坐标原点,F为抛物线y2=4x的焦点,A为抛物线上一点,若![]() =-4,
=-4,
则点A的坐标为( )
A.(2,±2![]() )
B.(1,±2)
C.(1,2) D.(2,2
)
B.(1,±2)
C.(1,2) D.(2,2![]() )
)
9.P为双曲线 =1的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1
=1的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1
上的点,则|PM|-|PN|的最大值为( )
A.6 B.7 C.8 D.9
三、解答题
21.(本小题满分12分)
如图,椭圆Q: =1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕
=1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕
点F转动,并且交椭圆于A、B两点,P为线段AB的中点.

(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令a2=1+cosθ+sinθ,b2=sinθ(0<θ≤![]() ).确定θ的值,使
).确定θ的值,使
原点距椭圆Q的右准线l最远.此时,设l与x轴交点为D,当直线m绕点F转动到
什么位置时,三角形ABD的面积最大?
陕西(理)
一、选择题(每小题5分)
5.设直线过点![]() 其斜率为1,且与圆
其斜率为1,且与圆![]() 相切,则
相切,则![]() 的值为()
的值为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7.已知双曲线 的两条渐近线的夹角为
的两条渐近线的夹角为![]() ,则双曲线的
,则双曲线的
离心率为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)2
(D)2
三、解答题
(21)(本小题满分为12分)
如图,三定点![]() 三动点D、E、M满足
三动点D、E、M满足
![]()
![]()
(I)求动直线DE斜率的变化范围;
(II)求动点M的轨迹方程。
安徽(理)
一、选择题(每题5分)
(3)若抛物线y2=2px的焦点与椭圆 的右焦点重合,则P的值为(
)
的右焦点重合,则P的值为(
)
(A)-2 (B)2 (C)-4 (D)4
(7)若曲线y=x4的一条切线l与直线![]() 垂直,则1的方程为(
)
垂直,则1的方程为(
)
(A)有最大值而无最小值 (B)有最小值而无最大值
(C)有最大值且有最小值 (D)即无最大值又无最小值
(22)(本小题满分14分)
如图,F为双曲线C: (a>0,b>0)的右焦点,P为双曲线C右支上一点,
(a>0,b>0)的右焦点,P为双曲线C右支上一点,
且位于x轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四
边形,|PF|=![]() |OF|。
|OF|。
(Ⅰ)写出双曲线C的离心率e与![]() 的关系式:
的关系式:
(Ⅱ)写![]() =1时,经过焦点F且平行于OP的直线交双曲线于A、B两点,若|AB|=
=1时,经过焦点F且平行于OP的直线交双曲线于A、B两点,若|AB|=
12,求此时的双曲线方程。

四川(理)
一、选择题(每小题5分)
(6)已知两定点![]() ,如果动点
,如果动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹
的轨迹
所包围的图形的面积等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(8)
某厂生产甲产品每千克需用原料![]() 和原料
和原料![]() 分别为
分别为![]() 千克,生产乙产品
千克,生产乙产品
每千克需用原料![]() 和原料
和原料![]() 分别为
分别为![]() 千克,甲、乙产品每千克可获利润分别
千克,甲、乙产品每千克可获利润分别
为![]() 元,月初一次性购进本月用原料
元,月初一次性购进本月用原料![]() 各
各![]() 千克,要计划本月生产甲产
千克,要计划本月生产甲产
品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月生
产甲、乙两种产品分别为![]() 千克,
千克,![]() 千克,月利润总额为
千克,月利润总额为![]() 元,那么,用于求使
元,那么,用于求使
总利润![]() 最大的数学模型中,约束条件为()
最大的数学模型中,约束条件为()
(A) (B)
(B) (C)
(C) (D)
(D)
(9)
直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过
两点,过![]() 两点向抛物线的准线
两点向抛物线的准线
作垂线,垂足分别为![]() ,则梯形
,则梯形![]() 的面积为()
的面积为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题(每小题4分)
(15)如图,把椭圆 的长轴
的长轴![]() 分成
分成![]() 等份,过每个分点作
等份,过每个分点作![]() 轴的
轴的
垂线交椭圆的上半部分于![]() 七个点,
七个点,![]() 是椭圆的一个焦点,
是椭圆的一个焦点,
则![]() ______________;
______________;

三、解答题
(21)(本小题满分14分)
已知两定点![]() ,满足条件
,满足条件![]() 的点
的点![]() 的轨迹
的轨迹
是曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,如果
两点,如果![]() ,
,
且曲线![]() 上存在点
上存在点![]() ,使,求
,使,求![]() 的值和
的值和![]() 的面积S。
的面积S。
全国卷(Ⅰ)理
一、选择题(每题5分)
(3)双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m=( )
(A)![]() (B)-4
(C)4
(D)
(B)-4
(C)4
(D)![]()
(8)抛物线y=-x2上的点到直线![]() 的距离的最小值是(
)
的距离的最小值是(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)3
(D)3
(9)设平面向量a1,a2,a3的和a1+a2+a3=0.如果平面各量b1,b2,b3满足
│bi│=2│ai│,且ai的顺时针旋转![]() 后与bi同向,其中i-1,2,3,则(
)
后与bi同向,其中i-1,2,3,则(
)
(A)-b1+b2+b3=0 (B)b1-b2+b3=0
(C)b1+b2-b3=0 (D)b1+b2+b3=0
(20)(本小题满分12分)
在平面直角坐标系xOy中,有一个以![]() 和
和![]() 为焦点、离心率为
为焦点、离心率为![]() 的
的
椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与x、y轴的
交点分别为A、B,且向量![]() ,求:
,求:
(Ⅰ)点M的轨迹方程;
(Ⅱ) 的最小值。
的最小值。
全国卷(Ⅱ)理
一、选择题(每小题5分)
(5)已知![]() 的顶点B、C在椭圆
的顶点B、C在椭圆 上,顶点A是椭圆的一个焦点,
上,顶点A是椭圆的一个焦点,
且椭圆的另外一个焦点在BC边上,则![]() 的周长是()
的周长是()
(A)![]() (B)6 (C)
(B)6 (C)![]() (D)12
(D)12
(9)已知双曲线 的一条渐近线方程为
的一条渐近线方程为![]() ,则双曲线的离心率为()
,则双曲线的离心率为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题(每小题4分)
(15)过点![]() 的直线
的直线![]() 将圆
将圆![]() 分成两段弧,当劣弧所对的
分成两段弧,当劣弧所对的
圆心角最小时,直线![]() 的斜率
的斜率![]() 解答
解答
三、解答题
(21)(本小题满分为14分)
已知抛物线![]() 的焦点为F,A、B是热线上的两动点,且
的焦点为F,A、B是热线上的两动点,且![]()
过A、B两点分别作抛物线的切线,设其交点为M。
(I)证明![]() 为定值;
为定值;
(II)设![]() 的面积为S,写出
的面积为S,写出![]() 的表达式,并求S的最小值。
的表达式,并求S的最小值。