三、解答题
(17)(本小题满分12分,第一小问满分5分,第二小问满分7分)
已知三点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0).
(6,0).
(Ⅰ)求以![]() 、
、![]() 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点P、![]() 、
、![]() 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为![]() 、
、![]() 、
、![]() ,
,
求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的双曲线的标准方程。
的双曲线的标准方程。
本小题主要考查椭圆与双曲线的基本概念、标准方程、几何性质等基础
知识和基本运算能力.满分12分.
解:(Ⅰ)由题意,可设所求椭圆的标准方程为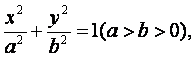
其半焦距c=6.
2a=|PF1|+|PF2|=![]()
∴a=3![]() ,b2=a2-c2=45-36=9.
,b2=a2-c2=45-36=9.
所以所求椭圆的标准方程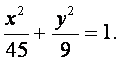
(Ⅱ)点P(5,2)、F1(-6,0)、F2(6,0)关于直线y=x的对称点
分别为P′(2,5)、F′1(0,-6)、F′2(0,6).
设所求双曲线的标准方程为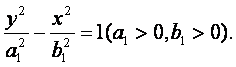
由题意知,半焦距c1=6,
2a1=||P′F′1||-|P′F′2||=![]()
∴a1=2![]() ,b21=c21-a21=36-20=16.
,b21=c21-a21=36-20=16.
所以所求双曲线的标准方程为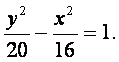
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。