(20) (本小题满分14分)
已知点![]() ,
,![]()
![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐
是坐
标原点,向量![]() ,
,![]() 满足
满足![]() .设圆
.设圆![]() 的方程为
的方程为
![]()
(I)
证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(II)当圆C的圆心到直线X-2Y=0的距离的最小值为时,求P的值。
本小题主要考查平面向量的基本运算,圆与抛物线的方程,点到直线的距离等基础
知识,以及综合运用解析几何知识解决问题的能力,满分14分.
(Ⅰ)证法一:∵![]()
∴(![]() )2=(
)2=(![]() )2,即
)2,即
![]() 整理得
整理得
![]() =0,
=0,
∴x1x2+y1y2=0. ①
设点M(x,y)是以线段AB为直径的圆上的任意一点,则
![]() =0.
=0.
即(x-x1)(x-x2)+(y-y1)(y-y2)=0.
展开上式并将①代入得
x2+y2-(x1+x2)x-(y1+y2)y=0.
故线段AB是圆C的直径.
证法二:∵![]()
∴![]()
![]() 整理得
整理得
![]() =0,
=0,
∴x1x2+y1y2=0. ①
若点(x,y)在以线段AB为直径的圆上,则
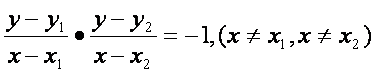
去分母得
(x-x1)(x-x2)+(y-y1)(y-y2)=0.
点(x1,y1),(x1,y2),(x2,y1),(x2,y2)满足上方程,展开并将①代入得
x2+y2-(x1+x2)x-(y1+y2)y=0.
所以在线段AB是圆C的直径.
证法三:∵![]()
∴(![]() )2=(
)2=(![]() )2,即
)2,即
![]() 整理得
整理得
![]() =0,
=0,
∴x1x2+y1y2=0. ①
以AB为直径的圆的方程是
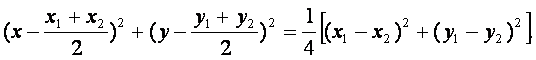
展开,并将①代入得
x2+y2-(x1+x2)x-(y1+y2)y=0.
所以线段AB是圆C的直径.
(Ⅱ)解法一:设圆C的圆心为C(x,y),则
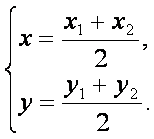
∵![]() =2px1,
=2px1,![]() =2px2(p>0).
=2px2(p>0).
∴x1x2=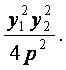
又∵x1x2+y1y2=0.
∴x1x2= -y1y2,
∴-y1y2=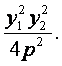
∵x1x2≠0,
∴y1y2≠0,
∴y1y2= -4p2.
∴x=

=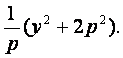
所以圆心的轨迹方程为:
y2=px-2p2.
设圆心C到直线x-2y=0的距离为d,则
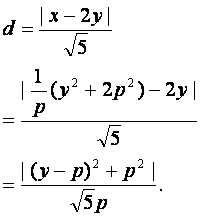
当y=P时,d有最小值![]() 由题设得
由题设得
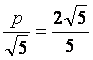 ,
,
∴p=2.
解法二:设圆C的圆心为C(x、y),则
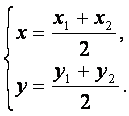
∵![]() =2px1,
=2px1,
![]() =2px2(p>0).
=2px2(p>0).
∴x1x2=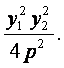
又∵x1x2+y1y2=0,
∴x1x2= -y1y2;
∵x1x2≠0.
∴y1y2= -4p2.
∵x=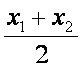

所以圆心的轨迹方程为
y2=px-2p2.
设直线x-2y+m=0与x-2y=0的距离为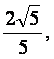 则
则
m=±2.
因为x-2y+2=0与y2=px-2p2无公共点.
所以当x-2y-2=0与y2=px-2p2仅有一个公共点时,该点到x-2y=0的距离最小,
最小值为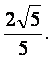

∴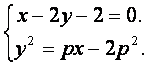
将②代入③得
y2-2py+2p2-2p=0,有
Δ=4p2- 4(2p2-2p)=0.
∵p>0,
∴p=2.
解法三:设圆C的圆心为C(x,y),则

若圆心C到直线x-2y=0的距离为d,那么
d=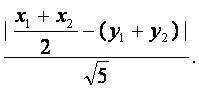
∵![]() =2px1,
=2px1,
![]() =2px2(p>0).
=2px2(p>0).
∴x1x2=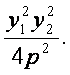
又∵x1x2+y1y2=0,
∴x1x2= -y1y2,
∵x1x2≠0.
∴y1y2=-4p2.
∴d=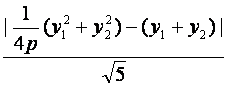
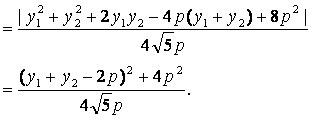
当y1+y2=2p时,d有最小值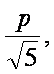 由题意得
由题意得
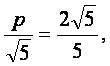
∴p=2.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。