三、解答题

(19)(本小题共14分)

    已知点M（-2，0)，N(2，0)，动点P满足条件|PM|-|PN|=2.记动点P的

轨迹为W.

    (Ⅰ)求W的方程；

    (Ⅱ)若A，B是W上的不同两点，O是坐标原点，求的最小值．

解法一：

   （Ⅰ）由|PM|-|PN|=2知动点P的轨迹是以M，N为焦点的双曲线的右支，

实半轴长a=.

        又半焦距c=2，故虚半轴长b=

所以W的方程为=1，x≥.

   （Ⅱ）设A，B的坐标分别为（x₁，y₁），（x₂，y₂）.

         当AB⊥x轴时，x₁=x₂，y₁= -y₂，从而=x₁x₂+y­₁y₂=x²₁-y²₁=2.

         当AB与x轴不垂直时，设直线AB的方程为y=kx+m，与W的方程联立，消去y得

（1-k²）x²-2kmx-m²-2=0，

         故x₁+x₂=

         所以

=x₁x₂+y­₁y₂

=x₁x₂+(kx₁+m)(kx₂+m)

=(1+k²)x₁x₂+km(x₁+x₂)+m²

        又因为x₁x₂＞0，所以k²-1＞0，从而＞2.

        综上，当AB⊥x轴时，取得最小值2.

解法二：

   （Ⅰ）同解法一.

   （Ⅱ）设A，B的坐标分别为（x₁，y₁），（x₂，y₂），则

x²_i- y²_i=( x_i+y_i)(x_i-y_i)=2(i=1,2).

令s_i=x_i+y_i，t_i=x_i-y_i，

    则s_it_i=2，且s_i＞0，t_i＞0，（i=1，2），所以

=x₁x₂+y₁y₂

   当且仅当s₁s₂=t₁t₂，即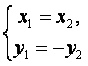时“=”成立.

   所以的最小值是2.