三、解答题

21.(本小题满分14分)

已知椭圆C₁:=1，抛物线C₂:(y-m)²=2px(p＞0)，且C₁、C₂的公共弦AB过椭圆

C₁的右焦点.

(Ⅰ)当AB⊥x轴时，求m、p的值，并判断抛物线C₂的焦点是否在直线AB上；

(Ⅱ)是否存在m、p的值，使抛物线C₂的焦点恰在直线AB上?若存在，求出符合条件的

m、p的值；若不存在，请说明理由．

解  (Ⅰ)当AB⊥x轴时，点A、B关于x轴对称，所以m=0，直线AB的方程为x=1，从而点A的坐标为(1，)或(1，-)．

因为点A在抛物线上，所以=2p，即p=.此时C₂的焦点坐标为(，0)，该焦点不在直线AB上．

（Ⅱ）解法一  假设存在m、p的值使C₂的焦点恰在直线AB上，由（Ⅰ）知直线AB的斜率存在，故可设直线AB的方程为y=k（x-1）.

由消去y得（3+4k²）x²-8k²x+4k²-12=0.                 ……①

设A、B的坐标分别为（x₁，y₁）、（x₂，y₂），则x₁、x₂是方程①的两根，x₁+x₂=.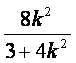

由消去y得

（kx-k-m）²=2px.                                               ……②

因为C₂的焦点F′（，m）在y=k（x-1）上，

所以m=k（-1），即m+k=.代入②有（kx-）²=2px.

即k²x²-p（k²+2）x+=0.                                  ……③

由于x₁、x₂也是方程③的两根，所以x₁+x₂=.

从而.               ……④

又AB过C₁、C₂的焦点，

所以|AB|=（x₁+）+（x₂+）=x₁+x₂+p=（2-x₁）+（2-），

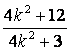则p=4-（x₁+x₂）=4-=.                    ……⑤

由④、⑤得=.

即k⁴-5k²-6=0.解得k²=6.

于是k=±，p=.

因为C₂的焦点F′（，m）在直线y=±（x-1）上，所以m=±（-1）.即m=或m=-.

由上知，满足条件的m、p存在，且m=或m=-，p=.

解法二  设A、B的坐标分别为（x₁，y₁）、（x₂，y₂），

因为AB即过C₁的右焦点F（1，0），又过C₂的焦点F′（，m），

所以|AB|=（x₁+）+（x₂+）=x₁+x₂+p=（2-x₁）+（2-x₂）.

即x₁+x₂=（4-p）.                                              ……①

由（Ⅰ）知x₁≠x₂，p≠2，于是直线AB的斜率k=，且直线AB的方程是y=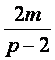（x-1）.                                            ……②

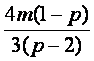所以y₁+y₂=（x₁+x₂-2）=.                           ……③

又因为，所以3（x₁+x₂）+4（y₁+y₂）·=0.     ……④

将①、②、③代入④得m²=.                        ……⑤

因为，所以y₁+y₂-2m=2p                   ……⑥

将②、③代入⑥得m²=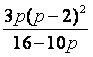.                                 ……⑦

由⑤、⑦得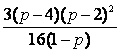=.即3p²+20p-32=0.

解得p=或p=-8（舍去）.

将p=代入⑤得m²=，所以m=或m=-.

由上知，满足条件的m、p存在，且m=或m=-，p=.