|
13.6.2平面与平面垂直<-->13.6.4空间中的距离
13.6.3空间中的角
(1)异面直线所成的角
①定义:$a,b$是两条异面直线,经过空间任意一点$O$,分别引直线$a'// a,b'//b$,则$a'$和$b'$所成的锐角(或直角)叫做异面直线a和b所成的角
②取值范围:$0°<\theta≤90°$.
③求解方法
a.根据定义,通过平移,找到异面直线所成的角$\theta$.
b.解含有角$\theta$的三角形,求出角0的大小.
(2)直线和平面所成的角
①直线和平面所成的角有三种:
a.斜线和平面所成的角
一条直线与平面$α$相交,但不和$α$垂直,则这条直线叫做平面$α$的斜线.斜线与$α$的交点叫做斜足,过斜线上斜足以外的点向平面引垂线,过垂足与斜足的直线叫做斜线在平面α内的射影.
平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.
b.垂线与平面所成的角:一条直线垂直于平面,则它们所成的角是直角.
c.一条直线和平面平行,或在平面内,则它们所成的角为 0°.
②)取值范围:$0°≤\theta≤90°$
③求解方法
a.作出斜线在平面上的射影,找到斜线与平面所成的角$\theta$.
b.解含角$\theta$的三角形,求出其大小.
④最小角定理
斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角.亦可说,斜线和平面所成的角不大于斜线与平面内任何直线所成的角.
拓展
①已知$PA$与$PB$分别是平面$\alpha$的垂线和斜线,在平面$α$内过斜足$B$任意引一直线$BC$
设$\angle PBA=\theta_1,\angle ABC=\theta_2,\angle PBC=\theta$,则有
$\cos \theta=\cos \theta_1·\cos \theta_2$.
②经过一个角的顶点作这个角所在平面的斜线,如果斜线和这个角两边的夹角相等,那么斜线在平面上的射影是这个角的平分线所在的直线
(3)二面角及二面角的平面角
①半平面:一条直线把平面分成两个部分,每部分都叫做半平面.
②二面角:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫二面角的棱,这两个半平面叫做二面角的面,即二面角由半平面-棱-半平面组成.
若两个平面相交,则以两个平面的交线为棱形成四个二面角.
二面角的大小用它的平面角来度量.二面角的取值范围是0°≤0≤180°.两个半平面重合时$\theta=0°$,共面时$\theta=180°$
③二面角的平面角
a.二面角的平面角:如图,在二面角$\alpha-l-\beta$的棱上任取一点$O$,以点$O$为垂足,在半平面$α$和$\beta$内分别作垂直于棱$l$的射线$OA$和$OB$,则射线$OA$和$OB$组成的$\angle AOB $叫做二面角的平面角.二面角的平面角范围是$[0°,180°]$.
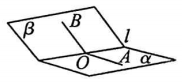
平面角是直角的二面角叫做直二面角.
b.二面角的平面角具有下列性质:
(a)二面角的棱垂直于它的平面角所在的平面,即$l\bot平面 AOB$.
(b)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.
(c)二面角的平面角所在的平面与二面角的两个面都垂直,即平面 $AOB\bot α,平面 AOB \bot \beta$.
c.求作二面角的平面角的常用方法见下表.

d.二面角的求法:
(a)通过二面角的平面角来求:
先找出或作出二面角的平面角,再证明其符合定义,然后通过解三角形,计算出二面角的平面角
上述过程可概括为“一作(找)、二证、三计算”
(b)利用面积射影定理求二面角的大小:
$S'=S·\cos \alpha$,
其中$S$为二面角的一个面内某个平面图形的面积,$S'$是这个平面图形在另一个面上的射影图形的面积,$α$为二面角的大小.
13.6.2平面与平面垂直<-->13.6.4空间中的距离
全网搜索"13.6.3空间中的角"相关
|

