|
13.6.3空间中的角<-->平面的斜线与射影
(1)点到平面的距离
①定义:从平面外一点引一个平面的垂线,这个点和垂足间的距离叫做这个点到这个平面的距离.
②)求点面距离常用的方法
a.直接利用定义求:
(a)找到(或作出)表示距离的线段;
(b)抓住线段(所求距离)所在三角形解之.
b.利用两平面互相垂直的性质.即如果已知点在已知平面的垂面上,则已知点到两平面交线的距离就是所求的点面距离.
c.体积法,其步骤是:在平面内选取适当三点和已知点构成三棱锥;求出此三棱锥的体积$V$和所取三点构成三角形的面积$S$;由$V=\dfrac{}{13}S·h$,求出$h$.这种方法的优点是不必作出垂线即可求点面距离,难点在于如何构造合适的三棱锥以便于计算.
d.转化法:将点到平面的距离转化为(平行)直线与平面的距离来求.
(2)直线和平面的距离
①定义:一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离.
a.直接利用定义求证(或连、或作)某线段为距离,然后通过解三角形计算之.
b.将线面距离转化为点面距离,然后运用解三角形或体积法求解之.
c.作辅助垂直平面,把求线面距离转化为求点线距离.
②)求线面距离常用的方法.
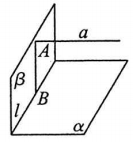
如图,若$a // α$,作$a$的垂面$\beta$,设垂足为$A$,找出$α$和$\beta$的交线,则点$A$到直线$l$的距离就等于$a$和平面$α4的距离.
(3)平行平面的距离
①定义:和两个平行平面同时垂直的直线,叫做这两个平行平面的公垂线.公垂线夹在两个平行平面间的部分,叫做这两个平行平面的公垂线段.
两个平行平面的公垂线段的长度叫做这两个平行平面的距离.
②)求平行平面距离常用的方法.
a.直接利用定义求证(或连、或作)某线段为距离,然后通过解三角形计算之.
b.把面面平行距离转化为线面平行距离,再转化为线线平行距离,最后转化为点线(面)距离,通过解三角形或体积法求解之
(4)异面直线的距离
①定义:与两条异面直线都垂直相交的直线叫做两条异面直线的公垂线.两条异面直线的公垂线在这两条异面直线间的线段的长度,叫做两条异面直线的距离.
任何两条确定的异面直线都存在唯一的公垂线段
②)求两条异面直线的距离常用的方法.
a.定义法:根据题目所给的条件,找出(或作出)两条异面直线的公垂线段,再根据有关定理、性质求出公垂线段的长.
此法一般多用于两异面直线互相垂直的情形.
b.转化法:转化为以下两种形式.
线面距离:找出过一条异面直线而与另一条异面直线平行的平面,则线面之间的距离即为所求.
面面距离:作出(或找出)两个平行平面,使两异面直线分别在两个平行平面内,则两平面之间的距离即为所求.
c.等体积法:根据已知条件,将异面直线间的距离视为某一几何体的高,然后利用同一几何体用两种方法求得的体积相等,从而求出异面直线的距离.
13.6.3空间中的角<-->平面的斜线与射影
全网搜索"13.6.4空间中的距离"相关
|

