|
13.6.1直线与平面垂直<-->13.6.3空间中的角
二面角
Ⅰ、二面角的概念:从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫二面角的棱,这两个半平面叫二面角的面。
Ⅱ、二面角的画法:
直立式:
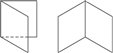
平卧式:

Ⅲ、二面角的表示:如图,

⑴如果棱为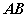 ,半平面为 ,半平面为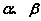 的二面角,可记作二面角 的二面角,可记作二面角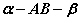 。 。
⑵如果在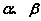 内(棱以外的半平面部分)分别取点 内(棱以外的半平面部分)分别取点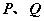 ,可将这个二面角记作二面角 ,可将这个二面角记作二面角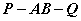 。 。
⑶如果棱为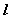 ,则这个二面角可记作 ,则这个二面角可记作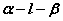 或 或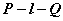 。 。
Ⅳ、二面角的求法:⑴通过求二面角的平面角;⑵用向量方法求二面角。
二面角的平面角
Ⅰ、二面角平面角的概念:
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
如右图所示,在二面角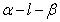 的棱l上任取一点O,以点O为垂足,在半平面 的棱l上任取一点O,以点O为垂足,在半平面 和 和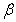 内分别作垂直于棱l的射线OA和OB,则射线OA和OB所成的∠AOB叫做二面角的平面角。 内分别作垂直于棱l的射线OA和OB,则射线OA和OB所成的∠AOB叫做二面角的平面角。
Ⅱ、二面角平面角的画法:
在二面角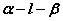 的棱上 的棱上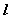 任取点O,以O为垂足,在半平面 任取点O,以O为垂足,在半平面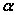 和 和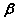 内分别 内分别
作垂直于棱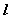 的射线 的射线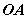 和 和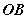 ,则射线 ,则射线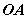 和 和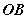 组成的 组成的 就是二面角 就是二面角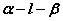 的平面角。 的平面角。
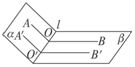
若再取棱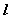 上另一点O′,在 上另一点O′,在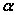 和 和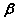 内分别作 内分别作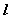 的垂线 的垂线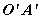 和 和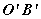 ,则它们组成角 ,则它们组成角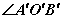 也是二面角 也是二面角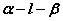 的平面角。 的平面角。
显然,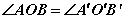 ,即二面角的平面角处处相等。 ,即二面角的平面角处处相等。
Ⅲ、二面角平面角的表示叙述:
∵ , ,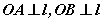 , ,
∴ 就是二面角 就是二面角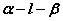 的平面角。 的平面角。
Ⅳ、二面角平面角的求法:找到二面角的平面角,利用解三角形求之。
二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度。平面角是直角的二面角叫做直二面角。
详解:
二面角的大小可以用它的平面角来度量,二面角的平面角是几度就说这个二面角是几度。
本书中,我们规定二面角的大小范围是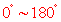 ,当二面角的两个面合成一个平面是,规定二面角的大小为 ,当二面角的两个面合成一个平面是,规定二面角的大小为 . .
若一个二面角的平面角是直角,就说这个二面角为直二面角。
二面角的平面角必须具备三个条件:
①角的顶点在二面角的棱上;
②角的两边分别在二面角的两个半平面内;
③角的两边分别与二面角的棱垂直。
平面与平面垂直的判定1.两平面互相垂直的定义:一般地,两个平面相交,如果它们所成的 二面角是直二面角,就说这两个平面互相垂直。 两个互相垂直的平面通常画成以下页图的样子,此时,把直立平面的竖边画成与水平平面的横边垂直。 平面α与β垂直,记作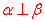 . .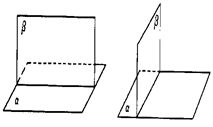 2.平面与平面垂直的判定 定理:一个平面过另一个平面的垂线,则这两个平面垂直。 符号语言: 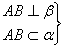 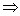 α⊥β。 图形语言: 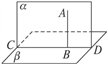
详解:
此定理常表述为:若线面垂直,则面面垂直。
此定理的作用是:证明面面垂直。
平面与平面垂直的性质
定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
用符号语言表示:已知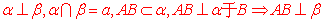
符号语言: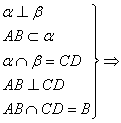 AB⊥β。 AB⊥β。
图形语言: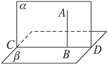
两个平面垂直的性质定理也可简述为:“面面垂直,则线面垂直”,它反映了面面垂直与线面垂直之间的密切关系。
详解:(1)这个定理说明,可以由直线与平面垂直证明平面与平面垂直。
(2)证明平面与平面垂直,还可以通过定义判断,即证二面角的平面角为直角。
(3)一个平面垂直于两个平行平面中的一个,也垂直于另一个。
(4)平面与平面垂直的性质定理说明,由平面与平面垂直可以得到直线与平面垂直。这种直线与平面的位置关系同平面与平面的位置关系的相互转化,是解决空间图形问题重要的思想方法。
(5)平面与平面垂直的性质定理实际上给出了证明线面垂直的又一种方法。
13.6.1直线与平面垂直<-->13.6.3空间中的角
全网搜索"13.6.2平面与平面垂直"相关
|

