|
13.5.4两个平面平行的性质<-->13.6.2平面与平面垂直
直线与平面垂直的定义
Ⅰ、直线与平面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α的垂直,记作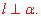 直线l叫做平面α的垂线,平面α叫做直线l的垂面。直线与平面垂直时,它们唯一的公共点P叫做垂足。 直线l叫做平面α的垂线,平面α叫做直线l的垂面。直线与平面垂直时,它们唯一的公共点P叫做垂足。
Ⅱ、直线与平面垂直的特点:过一点有且只有一条直线和一个平面垂直;过一点有且只有一个平面和一条直线垂直。
Ⅲ、直线与平面垂直的画法:
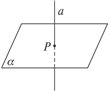
画图形时,注意横纵垂直。
Ⅳ、直线与平面垂直的表示:记作 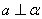 。 。
详解:
定义中的“任何一条直线”这一词语,它与“所有直线”是同义语,定义是说这条直线和平面内的所有直线都垂直。
直线和平面垂直时直线和平面相交的一种特殊形式。
虽然这样的定义给线面垂直的判定带来困难,但是在直线和平面垂直时,却可以得到直线和平面内任何一条直线都垂直,给判定两条直线垂直带来方便。
直线与平面垂直的判定
直线与平面垂直的判定:
定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
符号语言表述: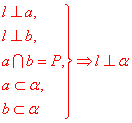
图形语言: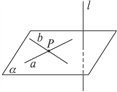
详解:
该定理常表述为“线线垂直,则线面垂直”。
该定理的作用:证明线面垂直。在应用该定理判定一条直线和一个平面垂直时,一定要抓住这条直线和平面内的两条相交直线,而不是任意的两条直线。
推论:如果在两条平行直线中,有一条垂直于平面,那么另一条直线也垂直于这个平面。用符号语言表述为:若 ,且 ,且 ,则 ,则 . .
证明线面垂直的方法证明线面垂直的 方法有: ⑴用定义:证明直线和平面内的 所有直线都垂直; ⑵用判定定理:证明直线与平面内的两条相交直线垂直,在用此定理时一定要 注意:①已知直线与两条直线都垂直;②两条直线都在所证的平面内;③这两条直线必须相交,这一条易被忽略。 ⑶利用判定定理的推论:即两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面; ⑷反证法:用此方法首先肯定直线与平面相交,再证明斜交不可能; ⑸同一法:这种方法在立体几何中是证题的重要手段,先作一条满足条件的平面的垂线,然后证明这条垂线就是要证的直线或说这条直线与所证直线是同一直线。
直线与平面垂直的性质
定理:垂直于同一个平面的两条直线平行。
符号语言: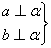 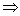 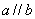
图形语言:
详解:
该定理的作用:证明线线平行
三个常见的结论:
1 若 ,且 ,且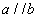 ,则 ,则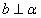 ; ;
2 过一点有且只有一条直线和已知平面垂直;
3 过一点有且只有一个平面和已知直线垂直。
垂直于同一条直线的两个平面平行。此结论也可以当做定理来使用。
如果两条平行线中有一条直线垂直于一个平面,那么另一条直线也垂直于这个平面。
平面的斜线与射影Ⅰ、平面的斜线:一条直线和一个平面相交,但不和这个平面垂直,这条直线就叫做 这个平面的斜线。斜线和平面的交点叫做斜足。(如图, 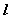 是平面 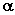 的斜线, 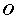 是斜足) 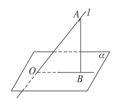 Ⅱ、平面的射影: Ⅱ、平面的射影: 从斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做 斜线在这个平面内的射影。(如图, 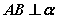 ,垂足 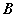 ,则直线 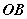 是斜线 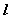 在平面 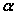 内的射影)
直线与平面所成的角定义:一条直线 PA和一个平面 α相交,但 不和这个平面 垂直,这条直线叫做这个平面的 斜线, 斜线和平面的交点A称之为斜足。 如图, 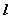 是平面 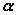 的一条斜线,点 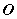 是斜足, 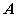 是 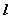 上任意一点, 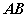 是平面 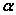 的垂线,点 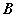 是垂足,那么直线 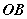 (记作 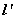 )是 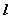 在平面 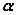 内射影,则 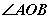 (记作 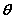 )是 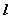 与平面  所成的角。 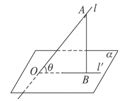 一条直线 垂于平面,我们说它们所成的角是 直角;一条直线和平面 平行或在平面内,我们说它们所成的角是 0°角。
详解:
当直线与平面平行时,直线与平面所成的角是0;当直线与平面垂直时,直线与平面所成的角是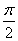 ,故直线与平面所成的角的取值范围是 ,故直线与平面所成的角的取值范围是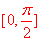 . .
证明线面垂直的方法
证明线面垂直的方法有:
⑴用定义:证明直线和平面内的所有直线都垂直;
⑵用判定定理:证明直线与平面内的两条相交直线垂直,在用此定理时一定要注意:①已知直线与两条直线都垂直;②两条直线都在所证的平面内;③这两条直线必须相交,这一条易被忽略。
⑶利用判定定理的推论:即两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面;
⑷反证法:用此方法首先肯定直线与平面相交,再证明斜交不可能;
⑸同一法:这种方法在立体几何中是证题的重要手段,先作一条满足条件的平面的垂线,然后证明这条垂线就是要证的直线或说这条直线与所证直线是同一直线。
|

