|
2020年高考数学新高考Ⅱ-20<-->2020年高考数学新高考Ⅱ-22
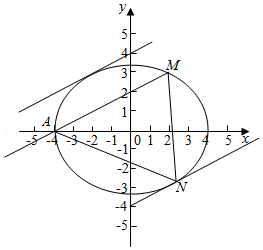
(12分)已知椭圆$C:\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1(a>b>0)$过点$M(2,3)$,点$A$为其左顶点,且$AM$的斜率为$\dfrac{1}{2}$.
(1)求$C$的方程;
(2)点$N$为椭圆上任意一点,求$\Delta AMN$的面积的最大值.
分析:
(1)利用已知条件求出$A$的坐标,然后求解$b$,得到椭圆方程.
(2)设出与直线$AM$平行的直线方程,与椭圆联立,利用判别式为0,求出椭圆的切线方程,然后求解三角形的最大值.
解答:(1)由题意可知直线$AM$的方程为:$y-3=\dfrac{1}{2}(x-2)$,
即$x-2y=-4$,
当$y=0$时,解得$x=-4$,所以$a=4$,
椭圆$C:\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1(a>b>0)$过点$M(2,3)$,
可得$\dfrac{4}{16}+\dfrac{9}{{b}^{2}}=1$,解得$b^{2}=12$,
所以$C$的方程:$\dfrac{{x}^{2}}{16}+\dfrac{{y}^{2}}{12}=1$.
(2)设与直线$AM$平行的直线方程为:$x-2y=m$,当直线与椭圆相切时,与$AM$距离比较远的直线与椭圆的切点为$N$,此时$\Delta AMN$的面积取得最大值.
$x-2y=m$代入椭圆方程:$\dfrac{{x}^{2}}{16}+\dfrac{{y}^{2}}{12}=1$.
化简可得:$16y^{2}+12my+3m^{2}-48=0$,所以△$=144m^{2}-4\times 16(3m^{2}-48)=0$,即$m^{2}=64$,解得$m=\pm 8$,
与$AM$距离比较远的直线方程:$x-2y=8$,
利用平行线之间的距离为:$d=\dfrac{8+4}{\sqrt{1+4}}=\dfrac{12\sqrt{5}}{5}$,
$\vert AM\vert =\sqrt{(2+4)^{2}+{3}^{2}}=3\sqrt{5}$.
所以$\Delta AMN$的面积的最大值:$\dfrac{1}{2}\times 3\sqrt{5}\times \dfrac{12\sqrt{5}}{5}=18$.
点评:本题考查直线与椭圆的位置关系的综合应用,椭圆方程的求法,椭圆的简单性质的应用,考查学生分析问题解决问题的数学素养,是中档偏难题.
2020年高考数学新高考Ⅱ-20<-->2020年高考数学新高考Ⅱ-22
全网搜索"2020年高考数学新高考Ⅱ-21"相关
|

