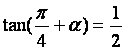
2004年
解答题
17.(本小题满分12分)
已知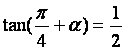
(1)求![]() 的值;(2)求
的值;(2)求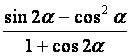 的值。
的值。
18.(本小题满分12分)
从4名男生和2名女生中任选3人参加演讲比赛。
(1)求所选3人都是男生的概率;
(2)求所选3人中恰有1名女生的概率;
(3)求所选3人中至少有1名女生的概率。
19.(本小题满分12分)
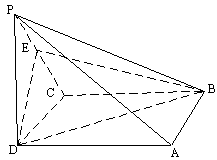
如图,在四棱锥![]() 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱![]() 底面ABCD,
底面ABCD,
![]() ,
,![]() 是PC的中点。
是PC的中点。
(1)证明![]() 平面EDB;(2)求EB与底面ABCD所成的角的正切值。
平面EDB;(2)求EB与底面ABCD所成的角的正切值。
20.(本小题满分12分)
设![]() 是一个公差为
是一个公差为![]() 的等差数列,它的前10项和
的等差数列,它的前10项和![]()
且![]() ,
,![]() ,
,![]() 成等比数列。
成等比数列。
(1)证明![]() ;(2)求公差
;(2)求公差![]() 的值和数列
的值和数列![]() 的通项公式。
的通项公式。
21.(本小题满分12分)
已知函数![]() 是R上的奇函数,当
是R上的奇函数,当![]() 时
时![]() 取得极值
取得极值![]() 。
。
(1)求![]() 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意![]() ,
,![]() ,不等式
,不等式![]() 恒成立。
恒成立。
22.(本小题满分14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点
,相应于焦点![]()
![]() 的
的
准线![]() 与
与![]() 轴相交于点A,
轴相交于点A,![]() ,过点A的直线与椭圆相交于P、Q两点。
,过点A的直线与椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;(2)若![]() ,求直线PQ的方程。
,求直线PQ的方程。
2005年
(17)(本小题满分12分)
已知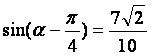 ,
,![]() ,求sina及
,求sina及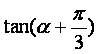
![]()
(18)(本小题满分12分)
若公比为c的等比数列![]() 的首项
的首项![]() 且满足
且满足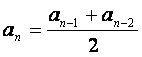 (n3,4,…)
(n3,4,…)![]()
(Ⅰ)求c的值;
(Ⅱ)求数列![]() 的前n项和
的前n项和![]()
![]()
(19)(本小题满分12分)
如图,在斜三棱柱![]() 中,
中,![]() ,
,
侧面![]() 与底面ABC所成的二面角为
与底面ABC所成的二面角为![]() ,E、F分别是棱
,E、F分别是棱![]() 的中点
的中点
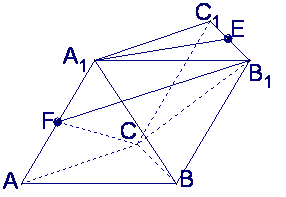 (Ⅰ)求
(Ⅰ)求![]() 与底面ABC所成的角
与底面ABC所成的角
(Ⅱ)证明![]() ∥平面
∥平面![]()
(Ⅲ)求经过![]() 四点的球的体积
四点的球的体积
(20)(本小题满分12)
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),
塔所在的山高OB=220(米),OA=200(米),
图中所示的山坡可视为直线![]() 且点P在直线
且点P在直线![]() 上,
上,
![]() 与水平地面的夹角为
与水平地面的夹角为![]() ,tan
,tan![]() =1/2试问此人
=1/2试问此人
距水平地面多高时,观看塔的视角∠BPC最大
(不计此人的身高)
(21)(本小题满分14分)
已知mÎR,设P:![]() 和
和![]() 是方程
是方程![]() 的两个实根,不等式
的两个实根,不等式
![]() 对任意实数
对任意实数![]() Î[-1,1]恒成立;
Î[-1,1]恒成立;
Q:函数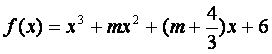 在(-¥,+¥)上有极值
在(-¥,+¥)上有极值![]()
求使P正确且Q正确的m的取值范围![]()
(22)(本小题满分14分)
抛物线C的方程为![]() ,过抛物线C上一点P(x0,y0)(x0¹0)作斜率
,过抛物线C上一点P(x0,y0)(x0¹0)作斜率
为k1,k2的两条直线分别交抛物线C于A(x1,y1)、B(x2,y2)两点(P、A、B三点
互不相同),且满足![]()
![]()
(Ⅰ)求抛物线C的焦点坐标和准线方程
(Ⅱ)设直线AB上一点M,满足![]() ,证明线段PM的中点在y轴上
,证明线段PM的中点在y轴上
(Ⅲ)当![]() =1时,若点P的坐标为(1,-1),求ÐPAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求ÐPAB为钝角时点A的纵坐标![]() 的取值范围
的取值范围
2006
解答题
(17)(本小题满分12分)
已知tanα+cotα=![]() ,α∈(
,α∈(![]() ,
,![]() ),求cos2α和sin(2α+
),求cos2α和sin(2α+![]() )的值.
)的值.
(18)(本小题满分12分)
甲、乙两台机床相互没有影响地生产某种产品,甲机床产品的正品率
是0.9,乙机床产品的正品率是0.95.
(Ⅰ)从甲机床生产的产品中任取3件,求其中恰有2件正品的概率
(用数字作答);
(Ⅱ)从甲、乙两台机床生产的产品中各任取1件,求其中至少有1件
正品的概率(用数字作答).
(19)(本小题满分12分)
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,
面CDE是等边三角形,棱EF![]()
![]() BC.
BC.
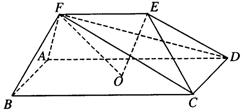
(Ⅰ)证明FO∥平面CDE;
(Ⅱ)设BC=![]() CD,证明EO⊥平面CDF
CD,证明EO⊥平面CDF
(20)(本小题满分12分)
已知函数f(x)=4x3-3x2cosθ+![]() ,其中x∈R,θ为参数,且0≤θ≤
,其中x∈R,θ为参数,且0≤θ≤![]() .
.
(Ⅰ)当cosθ=0时,判断函数f(x)是否有极值;
(Ⅱ)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数θ,函数f(x)在区间(2a-1,a)
内都是增函数,求实数a的取值范围.
(21)(本小题满分14分)
已知数列{xn}满足x1=x2=1,并且
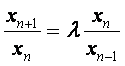 (
(![]() 为非零参数,n=2,3,4,…).
为非零参数,n=2,3,4,…).
(Ⅰ)若x1、x3、x5成等比数列,求参数λ的值;
(Ⅱ)设0<![]() <1,常数k∈N*且k≥3,证明
<1,常数k∈N*且k≥3,证明
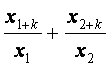 +…+
+…+ <
<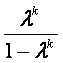 (n∈N*).
(n∈N*).
(22)(本小题满分14分)
如图,双曲线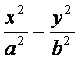 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为![]() ,F1、F2分别
,F1、F2分别
为左、右焦点,M为左准线与渐近线在第二象限内的交点,且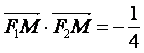 .
.
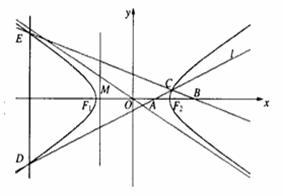
(Ⅰ)求双曲线的方程;
(Ⅱ)设A(m,0)和B(![]() ,0)
,0)![]()
是x轴上的两点.过点A作斜率不为0的
直线l,使得l交双曲线于C、D两点,
作直线BC交双曲线于另一点E.证明直线DE垂直于x轴.
2007
解答题
(17)(本小题满分12分)
在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求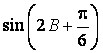 的值.
的值.
(18)(本小题满分12分)
已知甲盒内有大小相同的3个红球和4个黑球,乙盒内有大小相同的5个红球和
4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为红球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(19)(本小题满分12分)
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]()
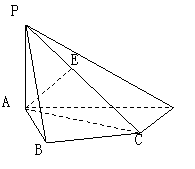
![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求![]() 和平面
和平面![]() 所成的角的大小;
所成的角的大小;
(Ⅱ)证明![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
(20)(本小题满分12分)
在数列![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明数列![]() 是等比数列;
是等比数列;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明不等式![]() ,对任意
,对任意![]() 皆成立.
皆成立.
(21)(本小题满分14分)
设函数![]() (
(![]() ),其中
),其中![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的极大值和极小值;
的极大值和极小值;
(Ⅲ)当![]() 时,证明存在
时,证明存在![]() ,使得不等式
,使得不等式![]() 对
对
任意的![]() 恒成立.
恒成立.
(22)(本小题满分14分)
设椭圆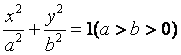 的左、右焦点分别为
的左、右焦点分别为![]() 是椭圆上的一点,
是椭圆上的一点,![]() ,
,
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)求![]() 使得下述命题成立:设圆
使得下述命题成立:设圆![]() 上任意点
上任意点![]() 处的切线交
处的切线交
椭圆于![]() ,
,![]() 两点,则
两点,则![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。