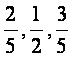 。现3人各投篮1次,求
。现3人各投篮1次,求2006
解答题
17.(本小题满分12分)
甲,乙,丙三人投篮,投进的概率分别是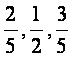 。现3人各投篮1次,求
。现3人各投篮1次,求
(Ⅰ)3人都投进的概率;
(Ⅱ)3人中恰有2人投进的概率。
(18)(本小题满分12分)
已知函数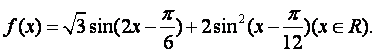
(I)求函数![]() 的最小正周期;
的最小正周期;
(II)求使函数![]() 取得最大值的
取得最大值的![]() 集合。
集合。
(19)(本小题满分12分)
如图,![]() 点A在直线
点A在直线![]() 上的射影为
上的射影为![]() 点B在
点B在![]() 上的射影为
上的射影为![]()
已知![]() 求:
求:
(I)直线AB分别与平面![]() 所成角的大小;
所成角的大小;
(II)二面角![]() 的大小。
的大小。
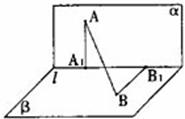
(第19题图)
20.(本小题满分12分)
已知正项数列![]() ,其前n项和Sn满足10Sn=
,其前n项和Sn满足10Sn=![]() +5an+6,
+5an+6,
且a1,a3,a15成等比数列,求数列![]() 的通项an.
的通项an.
(21)(本小题满分为12分)
如图,三定点![]() 三动点D、E、M满足
三动点D、E、M满足
![]()
![]()
(I)求动直线DE斜率的变化范围;
(II)求动点M的轨迹方程。
22.(本小题满分12分)
设![]() (k≥0)
(k≥0)
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)若函数![]() 的极小值大于0,求k的取值范围.
的极小值大于0,求k的取值范围.
2007
解答题
17.(本小题满分12分)
设函数![]() ,其中向量
,其中向量![]() ,
,![]() ,
,![]() ,且
,且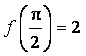 .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)求函数![]() 的最小值.
的最小值.
18.(本小题满分12分)
某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,
否则即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别
为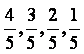 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手进入第四轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率.
(注:本小题结果可用分数表示)
19.(本小题满分12分)
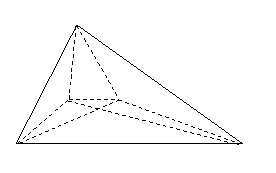 如图,在底面为直角梯形的四棱锥
如图,在底面为直角梯形的四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() .
.![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
20.(本小题满分12分)
已知实数列![]() 是等比数列,其中
是等比数列,其中![]() ,且
,且![]() ,
,![]() 成等差数列.
成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)数列![]() 的前
的前![]() 项和记为
项和记为![]() ,证明:
,证明:![]() .
.
21.(本小题满分12分)
已知![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数,
上是减函数,
又 .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若在区间![]() 上恒有
上恒有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
22.(本小题满分14分)
已知椭圆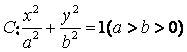 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
求![]() 面积的最大值.
面积的最大值.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。