2004年

解答题

17．（本小题满分12分）

等差数列{}的前n项和记为S_n.已知

（Ⅰ）求通项；

（Ⅱ）若S_n=242，求n.

解答

18．（本小题满分12分）

求函数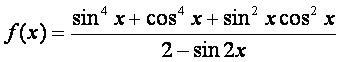的最小正周期、最大值和最小值.

解答

19．（本小题满分12分）

已知在R上是减函数，求的取值范围.

解答

20．（本小题满分12分）

从10位同学（其中6女，4男）中随机选出3位参加测验.每位女同学能通过

测验的概率均为，每位男同学能通过测验的概率均为.试求：

（I）选出的3位同学中，至少有一位男同学的概率；

（II）10位同学中的女同学甲和男同学乙同时被选中且通过测验的概率.

 解答

21．（本小题满分12分）

设是一常数，过点的直线与抛物线交于相异

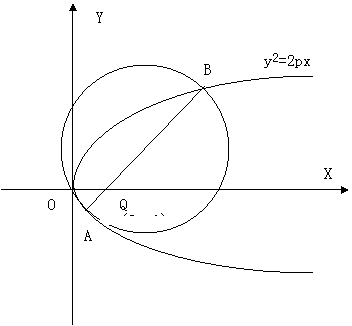
两点A、B，以线段AB为直经作圆H（H为圆心）。试证抛物线顶点

在圆H的圆周上；并求圆H的面积最小时直线AB的方程。

 解答

22．（本小题满分14分）

设双曲线C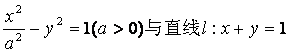：相交于两个不同的点A、B.

（I）求双曲线C的离心率e的取值范围：

（II）设直线l与y轴的交点为P，且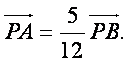求a的值.

解答

2005年

解答题

（17）（本大题满分12分）

设函数图像的一条对称轴是直线

（Ⅰ）求；

（Ⅱ）求函数的单调增区间；

（Ⅲ）画出函数在区间上的图像

解答

（18）（本大题满分12分）

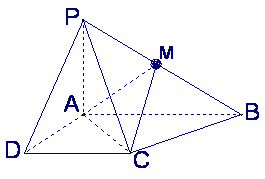已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，底面ABCD，

且PA=AD=DC=AB=1，M是PB的中点

（Ⅰ）证明：面PAD⊥面PCD；

（Ⅱ）求AC与PB所成的角；

（Ⅲ）求面AMC与面BMC所成二面角的大小

解答

（19）（本大题满分12分）

已知二次函数的二次项系数为，且不等式的解集为

（Ⅰ）若方程有两个相等的根，求的解析式；

（Ⅱ）若的最大值为正数，求的取值范围

解答

（20）（本大题满分12分）

9粒种子分种在甲、乙、丙3个坑内，每坑3粒，每粒种子发芽的概率为，若一个

坑内至少有1粒种子发芽，则这个坑不需要补种；若一个坑内的种子都没发芽，

则这个坑需要补种

（Ⅰ）求甲坑不需要补种的概率；

（Ⅱ）求3个坑中恰有1个坑不需要补种的概率；

（Ⅲ）求有坑需要补种的概率

（精确到）

解答

（21）（本大题满分12分）

设正项等比数列的首项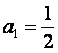，前n项和为，且

（Ⅰ）求的通项；

（Ⅱ）求的前n项和

解答

（22）（本大题满分14分）

已知椭圆的中心为坐标原点O，焦点在轴上，斜率为1且过椭圆右焦点F的

直线交椭圆于A、B两点，与共线

（Ⅰ）求椭圆的离心率；

（Ⅱ）设M为椭圆上任意一点，且，

证明为定值

解答

2006

解答题

(17)(本小题满分12分)

已知｛a｝为等比数列,a=2，a+a=.求｛a｝的通项公式.

解答

（18）（本小题满分12分）

的三个内角为A、B、C，求当A为何值时取得最大值，

并求出这个最大值。

解答

(19) (本小题满分12分)

A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验,每个试验组由4只小

白鼠组成,其中2只服用A,另2只服用B,然后观察疗效,若在一个试验组中,服用A有

效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A

有效的概率为,服用B有效的概率为.

(Ⅰ)求一个试验组为甲类组的概率；

(Ⅱ)观察3个试验组，求这3个试验组中至少有一个甲类组的概率.

解答

(20) (本小题满分12分)

如图，l、l是互相垂直的异面直线，MN是它们的公垂线段.点A、B在上l，

C在l上,AM=MB=MN.

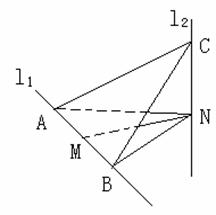
（Ⅰ）证明AC；

（Ⅱ）若，求NB与平面ABC所成角的余弦值.

解答

（21）（本小题满分12分）

设P是椭圆+y=1（a＞1）短轴一个端点，Q为椭圆上的一个动点，

求的最大值.

  解答

(22）（本小题满分14分）

设a为实数，函数f(x)=x-ax+(a-1)x在（-，0）和（1，+）都是增函数，

求a的取值范围.

    解答

2007年

解答题

（17）（本小题满分10分）

设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，．

（Ⅰ）求B的大小；

（Ⅱ）若，，求b．

解答

（18）（本小题满分12分）

某商场经销某商品，顾客可采用一次性付款或分期付款购买．根据以往资料统计，

顾客采用一次性付款的概率是0.6，经销一件该商品，若顾客采用一次性付款，

商场获得利润200元；若顾客采用分期付款，商场获得利润250元．

（Ⅰ）求3位购买该商品的顾客中至少有1位采用一次性付款的概率；

（Ⅱ）求3位顾客每人购买1件该商品，商场获得利润不超过650元的概率．

解答

（19）（本小题满分12分）

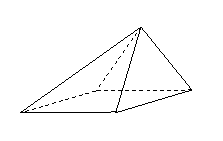四棱锥中，底面ABCD为平行四边形，侧面底面ABCD，

已知，，，．

（Ⅰ）证明：；

（Ⅱ）求直线SD与平面SBC所成角的大小．

解答

（20）（本小题满分12分）

设函数在及时取得极值．

（Ⅰ）求a、b的值；

（Ⅱ）若对于任意的，都有成立，求c的取值范围．

解答

（21）（本小题满分12分）

设是等差数列，是各项都为正数的等比数列，且，，

（Ⅰ）求，的通项公式；

（Ⅱ）求数列的前n项和．

解答

（22）（本小题满分12分）

已知椭圆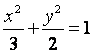的左、右焦点分别为，，过的直线交椭圆于B，D两点，

过的直线交椭圆于A，C两点，且，垂足为P．

（Ⅰ）设P点的坐标为，证明：；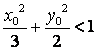

（Ⅱ）求四边形ABCD的面积的最小值．

解答