2004年
解答题
(17)(本小题满分12分)
已知6sin2α+sinαcosα-2cos2α=0,![]() ,求
,求![]() 的值。
的值。
(18)(本小题满分12分)
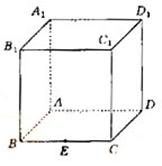 如图,在棱长为1的正方体ABCD-A1、B1、C1、D1中,点E是棱BC的中点,
如图,在棱长为1的正方体ABCD-A1、B1、C1、D1中,点E是棱BC的中点,
点F 是棱CD上的动点。
(Ⅰ)试确定点F的位置,使得D1E⊥平面AB1F;
(Ⅱ)当D1E⊥平面AB1F时,求二面角C1―EF―A的大小
(结果用反三角函数值表示)。
(19)(本小题满分12分)
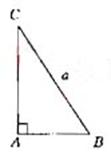 如图,在Rt△ABC中,已知BC=a,若长为2
a的线段P Q以点A为中点,
如图,在Rt△ABC中,已知BC=a,若长为2
a的线段P Q以点A为中点,
问![]() 与
与![]() 的夹角θ取何值时
的夹角θ取何值时![]() ,
,![]() 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。
(20)(本小题满分12分)
直线![]() :
:![]() 与双曲线C:
与双曲线C:![]() 的右支交于不同的两点A、B。
的右支交于不同的两点A、B。
(Ⅰ)求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在实数![]() ,使得以线段AB为直径的圆经过双曲线C的右焦点F?
,使得以线段AB为直径的圆经过双曲线C的右焦点F?
若存在,求出![]() 的值。若不存在,说明理由。
的值。若不存在,说明理由。
(21)(本小题满分12分)
某突发事件,在不采取任何预防措施的情况下发生的概率为0.3;一旦发生,
将造成400万元的损失。现有甲、乙两种相互独立的预防措施可供采用。
单独采用甲、乙预防措施所需的费用分别为45万元和30万元,采用相应预防
措施后此突发事件不发生的概率分别是0.9和0.85。若预防方案允许甲、乙
两种预防措施单独采用、联合采用或不采用,请确定预防方案使总费用最少。
(总费用=采取预防措施的费用+发生突发事件损失的期望值。)
(22)(本小题满分14分)
已知![]() ,数列
,数列![]() 满足
满足![]() n=1,2,…。
n=1,2,…。
![]()
(Ⅰ)已知数列![]() 极限存在且大于零,求A=
极限存在且大于零,求A=![]() (将A用
(将A用![]() 表示);
表示);
(Ⅱ)设![]() …,证明:
…,证明:![]() ;
;
(Ⅲ)若![]() 对
对![]() …,都成立,求
…,都成立,求![]() 的取值范围。
的取值范围。
2005年
解答题
17.(本小题满分12分)
已知向量a=(![]() ,x+1),b=
(1-x,t)
,x+1),b=
(1-x,t)![]() 若函数
若函数![]() =a·b在区间(-1,1)上
=a·b在区间(-1,1)上
是增函数,求t的取值范围![]()
18.(本小题满分12分)
在ΔABC中,已知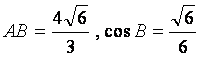 ,AC边上的中线BD=
,AC边上的中线BD=![]() ,求sinA的值
,求sinA的值
19.(本小题满分12分)
某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4次参加
考试的机会,一量某次考试通过,便可领取驾照,不再参加以后的考试,否则
就一直考到第4次为止![]() 如果李明决定参加驾照考试,设他每次参加考试通过的
如果李明决定参加驾照考试,设他每次参加考试通过的
概率依次为0.6,0.7,0.8,0.9![]() 求在一年内李明参加驾照考试次数
求在一年内李明参加驾照考试次数![]() 的分布列
的分布列
和![]() 的期望,并求李明在一所内领到驾照的概率
的期望,并求李明在一所内领到驾照的概率
20.(本小题满分12分)
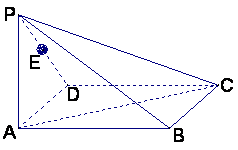 如图,在四棱锥P—ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,
如图,在四棱锥P—ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,
AB=![]() ,BC=1,PA=2,E为PD的中点
,BC=1,PA=2,E为PD的中点![]()
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,
并求出N点到AB和AP的距离![]()
21.(本小题满分12分)
设A、B是椭圆![]() 上的两点,点N(1,3)是线段AB的中点,线段AB的
上的两点,点N(1,3)是线段AB的中点,线段AB的
垂直平分线与椭圆相交于C、D两点![]()
(Ⅰ)确定![]() 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的![]() ,使得A、B、C、D四点在同一个圆上?并说明理由
,使得A、B、C、D四点在同一个圆上?并说明理由![]()
22.(本小题满分14分)
已知不等式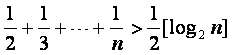 ,其中n为大于2的整数,
,其中n为大于2的整数,![]() 表示
表示
不超过![]() 的最大整数
的最大整数![]() 设数列{
设数列{![]() }的各项为正,且满足
}的各项为正,且满足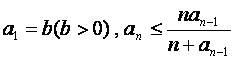 ,
,
![]()
![]()
(Ⅰ)证明: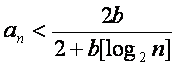 ,
,![]() ;
;
(Ⅱ)猜测数列{![]() }是否有极限?如果有,写出极限的值;
}是否有极限?如果有,写出极限的值;
(Ⅲ)试确定一个正整数N,使得当n>N时,对任意b>0,都有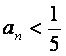
![]()
2006
解答题
16.(本小题满分12分)
设函数![]() ·(b+c),其中向量a=(sinx,—cosx),b=(sinx,—3cosx),
·(b+c),其中向量a=(sinx,—cosx),b=(sinx,—3cosx),
c=(—cosx,sinx),x![]() 。
。
(Ⅰ)求函数f(x)的最大值和最小正周期;
(Ⅱ)将函数y=f(x)的图像按向量d平移,使平移后得到的图象关于坐标
原点成中心对称,求长度最小的d。
17.(本小题满分13分)
已知二次函数y=f(x)的图象经过坐标原点,其导函数为![]() .数列{
.数列{![]() }的
}的
前n项和为Sn,点![]() 均在函数y=f(x)的图象上。
均在函数y=f(x)的图象上。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有
对所有![]() 都成
都成
立的最小正整数m。
18.(本小题满分12分)
如图,在棱长为1的正方体ABCD—A1B1C1D1中,P是侧棱CC1上的一点,CP=m。
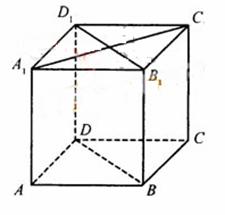
(Ⅰ)试确定m,使得直线AP与平面BDD1B1所成角的正切值为![]() ;
;
(Ⅱ)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影
垂直于AP,并证明你的结论。
19.(本小题满分10分)
在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布N(70,100)。
已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)试问此次参赛的学生总数约为多少人?
(Ⅱ)若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
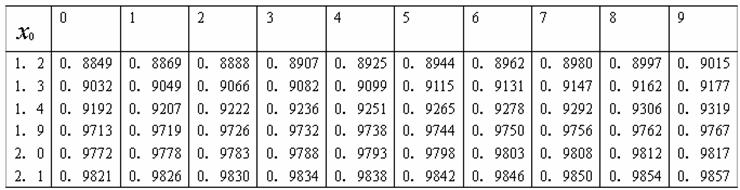
可供查阅的(部分)标准正态分布表![]() (x0)=P(x<x0)
(x0)=P(x<x0)
20.(本小题满分14分)
设A、B分别为椭圆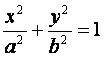 (a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
(a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
且x=4为它的右准线。
(Ⅰ)求椭圆的方程;
(Ⅱ)设P为右准线上不同于点(4,0)的任意一点,若直线AP、BP分别与椭圆相交于
异于A、B的点M、N,证明点B在以MN为直径的圆内。
(此题不要求在答题卡上画图)
21.(本小题满分14分)
设x=3是函数f(x)=(x2+ax+b)e3-x(x∈R)的一个极值点。
(Ⅰ)求a与b的关系式(用a表示b),并求f(x)的单调区间;
(Ⅱ)设![]() >0,
>0,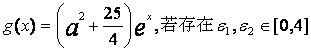 使得
使得![]() <1成立,
<1成立,
求a的取值范围。
2007年
解答题
16.(本小题满分12分)
已知![]() 的面积为
的面积为![]() ,且满足
,且满足![]() ,设
,设![]() 和
和![]() 的夹角为
的夹角为![]() .
.
(I)求![]() 的取值范围;
的取值范围;
(II)求函数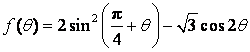 的最大值与最小值.
的最大值与最小值.
17.(本小题满分12分)
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,
将数据分组如表:
|
分组 |
频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
(I)在答题卡上完成频率分布表,并在给定的坐标系
中画出频率分布直方图;
(II)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]()
的概率是多少?
(III)统计方法中,同一组数据常用该组区间的中点值
(例如区间![]() 的中点值是
的中点值是![]() )作为代表.据此,
)作为代表.据此,
估计纤度的期望.
18.(本小题满分12分)
如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
![]()
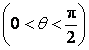 .
.
(I)求证:平面![]()
![]() ;
;
(II)当解![]() 变化时,求直线
变化时,求直线![]() 与平面
与平面![]() 所成的角的取值范围.
所成的角的取值范围.

19.(本小题满分12分)
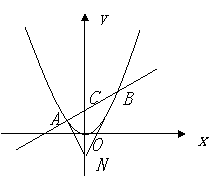
在平面直角坐标系![]() 中,过定点
中,过定点![]() 作直线与抛物线
作直线与抛物线![]() (
(![]() )相交于
)相交于![]() 两点.
两点.
(I)若点![]() 是点
是点![]() 关于坐标原点
关于坐标原点![]() 的对称点,求
的对称点,求![]() 面积的最小值;
面积的最小值;
(II)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?
为直径的圆截得的弦长恒为定值?
若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(此题不要求在答题卡上画图)
20.(本小题满分13分)
已知定义在正实数集上的函数![]() ,
,![]() ,其中
,其中![]() .
.
设两曲线![]() ,
,![]() 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用![]() 表示
表示![]() ,并求
,并求![]() 的最大值;
的最大值;
(II)求证:![]() (
(![]() ).
).
21.(本小题满分14分)
已知![]() 为正整数,
为正整数,
(I)用数学归纳法证明:当![]() 时,
时,![]() ;
;
(II)对于![]() ,已知
,已知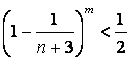 ,求证
,求证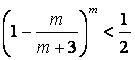 ,
,
求证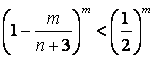 ,
,![]() ;
;
(III)求出满足等式![]() 的所有正整数
的所有正整数![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。