2004年

解答题

17．（本小题满分12分）

    求函数的取小正周期和取小值；

并写出该函数在上的单调递增区间。

解答

18．（本小题满分12分）

设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5。

（1）    三人各向目标射击一次，求至少有一人命中目标的概率及恰有

两人命中目标的概率；

    （2） 若甲单独向目标射击三次，求他恰好命中两次的概率。

解答

19．（本小题满分12分） 

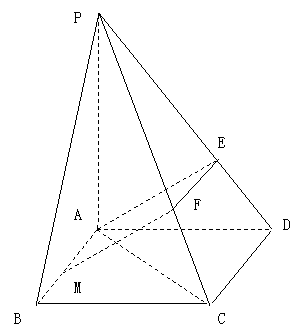
如图，四棱锥P-ABCD的底面是正方形，

(1)  证明MF是异面直线AB与PC的公垂线；

(2)  若,求直线AC与平面EAM所成角的正弦值。

解答

20．（本小题满分12分）

     某工厂生产某种产品，已知该产品的月生产量（吨）与每吨产品的价格

（元/吨）之间的关系式为：,且生产x吨的成本为（元）。

问该产每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）

解答

21．（本小题满分12分）

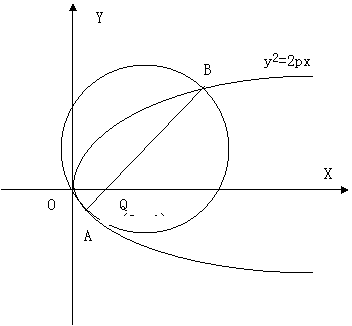
设是一常数，过点的直线与抛物线交于相异

两点A、B，以线段AB为直经作圆H（H为圆心）。试证抛物线顶点

在圆H的圆周上；并求圆H的面积最小时直线AB的方程。

22．（本小题满分14分）

      设数列满足:

(1)     令求数列的通项公式；

(2)  求数列的前n项和。

解答

2005年

解答题

17．（本小题满分13分）

若函数的最大值为，试确定常数a

的值.

     解答

18．（本小题满分13分）

加工某种零件需经过三道工序，设第一、二、三道工序的合格率分别为、、，

且各道工序互不影响.

   （Ⅰ）求该种零件的合格率；

   （Ⅱ）从该种零件中任取3件，求恰好取到一件合格品的概率和至少取到一件合格品的

 概率.

解答

19．（本小题满分13分）

设函数R.

（1）若处取得极值，求常数a的值；

（2）若上为增函数，求a的取值范围.

解答

20．（本小题满分13分）

  如图，在四棱锥P—ABCD中，底面ABCD为矩形，PD⊥底面ABCD，E是AB上一点，

  PE⊥EC. 已知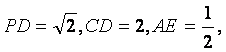求

   （Ⅰ）异面直线PD与EC的距离；

   （Ⅱ）二面角E—PC—D的大小.

解答

21．（本小题满分12分）

已知中心在原点的双曲线C的右焦点为（2，0），右顶点为

   （1）求双曲线C的方程；

   （2）若直线与双曲线C恒有两个不同的交点A和B，且

（其中O为原点）. 求k的取值范围.

     解答

22．（本小题满分12分）

数列记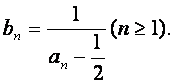

    （Ⅰ）求b1、b2、b3、b4的值；

    （Ⅱ）求数列的通项公式及数列的前n项和

解答

2006

（17）（本小题满分13分）

甲、乙、丙三人在同一办公室工作，办公室里只有一部电话机，

设经该机打进的电话

是打给甲、乙、丙的概率依次为、、.若在一段时间内打进

三个电话，且各个电话相互独立.

求：

(Ⅰ)这三个电话是打给同一个人的概率；

(Ⅱ)这三个电话中恰有两个是打给甲的概率.

  解答

（18）（本小题满分13分）

函数f（x）=cos²ωx+sinωxcosωx+a（其中ω＞0，a∈R），且f（x）的

图象在y轴右侧的第一个最高点的横坐标为.

(Ⅰ)求ω的值：

(Ⅱ)如果f（x）在区间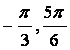［］上的最小值为，求a的值.

      解答

(19)（本小题满分12分）

设函数f（x）=x³－3ax²+3bx的图象与直线12x+y-1=0相切于点（1，－11）.

(Ⅰ)求a，b的值；

(Ⅱ)讨论函数f（x）的单调性.

解答

(20)（本小题满分12分）

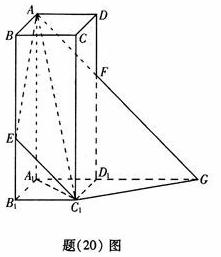
如图，在正四棱柱ABCD-A₁B₁C₁D₁中：AB=1，BB₁=+1，E为BB₁上

使B₁E=1的点，平面AEC₁交DD₁于F，交A₁D₁的延长线于G.求：

（Ⅰ）异面直线AD与C₁G所成的角的大小；

（Ⅱ）二面角A-C₁G-A₁的正切值.

        解答

（21）（本小题满分12分）

已知定义域为R的函数f（x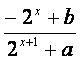）=是奇函数.

(Ⅰ)求a，b的值；

(Ⅱ)若对任意t∈R，不等式f（t²-2t）+f（2t²-k）＜0恒成立，

求k的取值范围.

解答

(22)（本小题满分12分）

如图，对每个正整数n，A_n（x_n，y_n）是抛物线x²=4y上的点，

过焦点F的直线FA.交抛物线于另一点B_n（s_n，t_n）.

解答

2007年

解答题

17．（本小题满分13分．（Ⅰ）小问5分．（Ⅱ）小问8分．）

       设甲、乙两人每次射击命中目标的概率分别为和，且各次射击相互独立．

（Ⅰ）若甲、乙各射击一次，求甲命中但乙未命中目标的概率；

（Ⅱ）若甲、乙各射击两次，求两人命中目标的次数相等的概率．

解答

18．（本小题满分13分，（Ⅰ）小问4分，（Ⅱ）小问9分）

已知函数．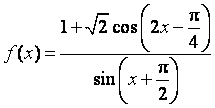

（Ⅰ）求的定义域；

（Ⅱ）若角在第一象限且，求．

解答

19．（本小题满分12分，（Ⅰ）小问6分，（Ⅱ）小问6分）

如题19图，在直三棱柱中，，

；点在棱上，

；，垂足为，求：

（Ⅰ）异面直线与的距离；

（Ⅱ）四棱锥的体积．

解答

20．（本小题满分12分）

用长为18m的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为，

问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？

解答

21．（本小题满分12分，（Ⅰ）小问4分，（Ⅱ）小问8分）

如题21图倾斜角为的直线经过抛物线的焦点，

且与抛物线交于两点．

（Ⅰ）求抛物线的焦点的坐标及准线的方程；

（Ⅱ）若为锐角，作线段的垂直平分线

交轴于点，证明为定值，

并求此定值．

解答

22．（本小题满分12分，（Ⅰ）小问5分，（Ⅱ）小问7分）

已知各项均为正数的数列的前项和满足，

且．

（Ⅰ）求的通项公式；

（Ⅱ）设数列满足，并记为的前项和，

求证：．

解答