解答题
全国卷Ⅰ(理)
(18)(本小题满分12分)
某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
|
|
1 |
2 |
3 |
4 |
5 |
|
|
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润
为250元;分4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求事件![]() :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率![]() ;
;
(Ⅱ)求![]() 的分布列及期望
的分布列及期望![]() .
.
全国卷Ⅱ(理)
18.(本小题满分12分)
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件![]() :
:
“取出的2件产品中至多有1件是二等品”的概率![]() .
.
(1)求从该批产品中任取1件是二等品的概率![]() ;
;
(2)若该批产品共100件,从中任意抽取2件,![]() 表示取出的2件产品中
表示取出的2件产品中
二等品的件数,求![]() 的分布列.
的分布列.
北京卷(理)
16.(本小题共14分)
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以
以
直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角.动点
是直二面角.动点![]() 的斜边
的斜边![]() 上.
上.
(I)求证:平面![]() 平面
平面![]() ;
;
(II)当![]() 为
为![]() 的中点时,求异面直线
的中点时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(III)求![]() 与平面
与平面![]() 所成角的最大值.
所成角的最大值.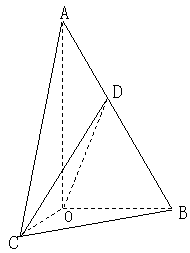
天津卷(理)
18.(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和
4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设![]() 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
上海卷(理)
17.(本题满分14分)
在![]() 中,
中,![]() 分别是三个内角
分别是三个内角![]() 的对边.若
的对边.若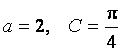 ,
,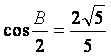 ,
,
求![]() 的面积
的面积![]() .
.
辽宁卷(理)
18.(本小题满分12分)
如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() 的中点,
的中点,
![]() 为棱
为棱![]() 上的点,二面角
上的点,二面角![]() 为
为![]() .
.
(I)证明:![]() ;
;
(II)求![]() 的长,并求点
的长,并求点![]() 到平面
到平面![]() 的距离.
的距离.
江苏卷
18.(本题满分12分)
如图,已知![]() 是棱长为
是棱长为![]() 的正方体,
的正方体,
点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证:![]() 四点共面;(4分)
四点共面;(4分)
(2)若点![]() 在
在![]() 上,
上,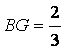 ,点
,点![]() 在
在![]() 上,
上,
![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() 平面
平面![]() ;(4分)
;(4分)
(3)用![]() 表示截面
表示截面![]() 和侧面
和侧面![]() 所成的锐二面角的大小,求
所成的锐二面角的大小,求![]() .(4分)
.(4分)
浙江卷(理)
(19)(本题14分)在如图所示的几何体中,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(I)求证:![]() ;
;
(II)求![]() 与平面
与平面![]() 所成的角.
所成的角.
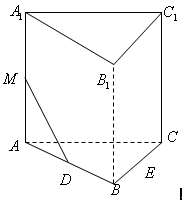
福建卷(理)
18.(本小题满分12分)
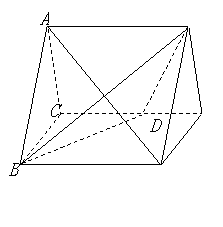 如图,正三棱柱
如图,正三棱柱![]() 的所有棱长都为
的所有棱长都为
![]() ,
,![]() 为
为![]() 中点.
中点.
![]()
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
C1
的大小;
C1
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
B1
的距离.
B1
湖北卷(理)
17.(本小题满分12分)
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,
将数据分组如表:
|
分组 |
频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
(I)在答题卡上完成频率分布表,并在给定的坐标系
中画出频率分布直方图;
(II)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]()
的概率是多少?
(III)统计方法中,同一组数据常用该组区间的中点值
(例如区间![]() 的中点值是
的中点值是![]() )作为代表.据此,
)作为代表.据此,
估计纤度的期望.
湖南卷(理)
17.(本小题满分12分)
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,
每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加
过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选
择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,记![]() 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求![]() 的分布列和期望.
的分布列和期望.
广东卷(理)
17.(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与
(吨)与
相应的生产能耗![]() (吨标准煤)的几组对照数据.
(吨标准煤)的几组对照数据.
|
|
3 |
4 |
5 |
6 |
|
|
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技改前![]() 吨甲产品的生产能耗为
吨甲产品的生产能耗为![]() 吨标准煤.试根据(2)求出
吨标准煤.试根据(2)求出
的线性回归方程,预测生产![]() 吨甲产品的生产能耗比技改前降低多少吨标准煤?
吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:![]() )
)
重庆卷(理)
18.(本小题满分13分,其中(Ⅰ)小问4分,(Ⅱ)小问9分)
某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆![]() 元的保险金,
元的保险金,
对在一年内发生此种事故的每辆汽车,单位可获![]() 元的赔偿(假设每辆车最多只赔
元的赔偿(假设每辆车最多只赔
偿一次),设这三辆车在一年内发生此种事故的概率分别为![]() ,
,![]() ,
,![]() ,且各车是否
,且各车是否
发生事故相互独立,求一年内该单位在此保险中:
(Ⅰ)获赔的概率;
(Ⅱ)获赔金额![]() 的分布列与期望.
的分布列与期望.
山东卷(理)
(18)(本小题满分12分)
设![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量![]() 表示方程
表示方程![]()
实根的个数(重根按一个计).
(Ⅰ)求方程![]() 有实根的概率;
有实根的概率;
(Ⅱ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程![]() 有实根的概率.
有实根的概率.
江西卷(理)
18.(本小题满分12分)
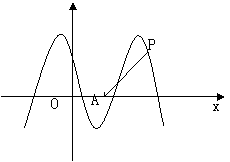 如图,函数
如图,函数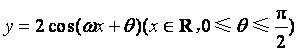 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,
且在该点处切线的斜率为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
![]()
(2)已知点 ,点
,点![]() 是该函数图象上一点,
是该函数图象上一点,
点![]() 是
是![]() 的中点,当
的中点,当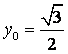 ,
,![]() 时,求
时,求![]() 的值.
的值.
陕西卷(理)
18.(本小题满分12分)
某项选拔共有四轮考核,每轮设有一问题,能正确回答问题者进入下一轮考核,
否则即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别
为![]() 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选择中回答问题的个数记为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
(注:本小题结果可用分数表示)
四川卷(理)
(18)(本小题满分12分)厂家在产品出厂前,需对产品做检验,厂家将一批
产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定
是否接收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.
求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任
取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可
能检验出不合格产品数![]() 的分布列及期望
的分布列及期望![]() ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
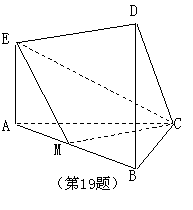
安徽卷(理)
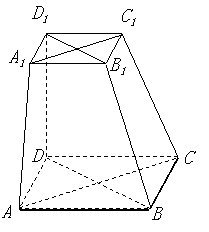 17.(本小题满分14分)
17.(本小题满分14分)
如图,在六面体![]() 中,四边形
中,四边形![]() 是边长为
是边长为
2的正方形,四边形![]() 是边长为1的正方形,
是边长为1的正方形,![]() 平面
平面
![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
(Ⅰ)求证:![]() 与
与![]() 共面,
共面,![]() 与
与![]() 共面.
共面.
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小(用反三角函数值表示).
的大小(用反三角函数值表示).
海南宁夏卷(理)
18.(本小题满分12分)
如图,在三棱锥![]() 中,侧面
中,侧面![]() 与侧面
与侧面![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() 为
为![]() 中点.
中点.
(Ⅰ)证明:![]() 平面
平面![]() ;
;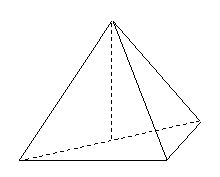
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。