解答题

 全国卷Ⅰ(理)

（19）（本小题满分12分）

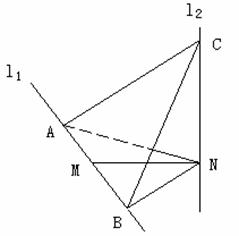
如图，l₁、l₂是互相垂直的异面直线，MN是它们的公垂线段，点A、B在l₁上，C在

l₂上，AM=MB=MN。

（Ⅰ）证明；

（Ⅱ）若，求NB与平面ABC所成角的余弦值。

解答

全国卷Ⅱ(理)

（19）（本小题满分１２分）

  如图，在直三棱柱中，、分别为、的中点。

       （I）证明：ED为异面直线与的公垂线；

       （II）设求二面角的大小。

         解答

北京卷(理)

（17）（本小题共14分）

如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，

且PA=AB，点E是PD的中点.

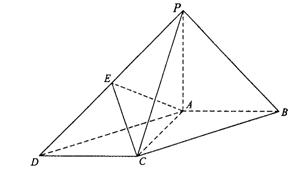
（Ⅰ）求证：AC⊥PB；

（Ⅱ）求证：PB∥平面AEC；

（Ⅲ）求二面角E-AC-B的大小.

解答

天津卷(理)

 (19)(本小题满分12分)

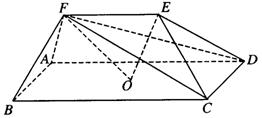
如图，在五面体ABCDEF中，点O是矩形ABCD的对角线的交点，

面CDE是等边三角形，棱EFBC．

  (Ⅰ)证明FO∥平面CDE；

(Ⅱ)设BC=CD，证明EO⊥平面CDF.

解答

上海卷(理)

19．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分）

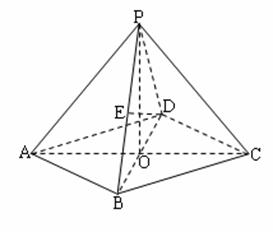
在四棱锥P－ABCD中，底面是边长为2的菱形，∠DAB＝60，对角线AC与BD

相交于点O，PO⊥平面ABCD，PB与平面ABCD所成的角为60．

（1）求四棱锥P－ABCD的体积；

（2）若E是PB的中点，求异面直线DE与PA所成角的大小（结果用反三角函数值表示）．

解答

辽宁卷

(19) (本小题满分12分)

现有甲、乙两个项目，对甲项目每投资十万元，一年后利润是1.2万元、1.18万元、

1.17万元的概率分别为、、;已知乙项目的利润与产品价格的调整有关,在每

次调整中,价格下降的概率都是,设乙项目产品价格在一年内进行2次独立

的调整,记乙项目产品价格在一年内的下降次数为,对乙项目每投资十万元, 取

0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量、分别

表示对甲、乙两项目各投资十万元一年后的利润.

(I)  求、的概率分布和数学期望、;

(II)  当时,求的取值范围.

解答

     江苏卷

（19）（本小题满分14分，第一小问满分4分，第二小问满分5分，

     第三小问满分5分）

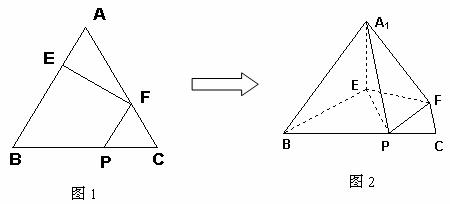
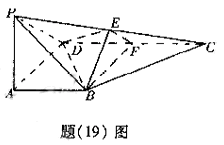
　　　在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足

     AE:EB＝CF:FA＝CP:PB＝1:2（如图1）。将△AEF沿EF折起到的位置，

     使二面角A₁－EF－B成直二面角，连结A₁B、A₁P（如图2）

   （Ⅰ）求证：A₁E⊥平面BEP；

（Ⅱ）求直线A₁E与平面A₁BP所成角的大小；

（Ⅲ）求二面角B－A₁P－F的大小（用反三角函数表示）

解答

浙江卷(理)

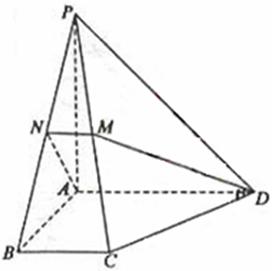
（17）如图，在四棱锥P-ABCD中，底面为直角梯形，AD//BC，BAD=，

PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点.

     （Ⅰ）求证：PB⊥DM；

     （Ⅱ） 求CD与平面ADMN所成的角。

 解答

福建卷(理)

（19）（本小题满分12分）

 统计表明，某种型号的汽车在匀速行驶中每小时的耗油量（升）关于行驶

速度（千米/小时）的函数解析式可以表示为：

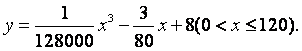已知甲、乙两地相距100千米。

（I）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？

（II）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？

解答

湖北卷(理)

18．（本小题满分12分）

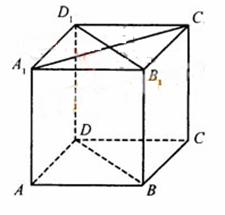
   如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，P是侧棱CC₁上的一点，CP=m。

（Ⅰ）试确定m，使得直线AP与平面BDD₁B₁所成角的正切值为；

（Ⅱ）在线段A₁C₁上是否存在一个定点Q，使得对任意的m，D₁Q在平面APD₁上的射影

垂直于AP，并证明你的结论。

解答

湖南卷(理)

18．(本小题满分14分)

    如图4，己知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2，AB=4．

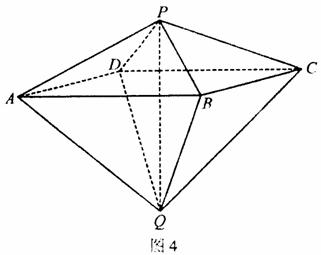
    (Ⅰ)证明PQ⊥平面ABCD；

    (Ⅱ)求异面直线AQ与PB所成的角；

    (Ⅲ)求点P到平面QAD的距离．

解答     

广东卷

17．（本小题满分14分）

    如图所示，AF、DE分别是⊙、⊙₁的直径。AD与两圆所在的平面均

垂直，AD=8，BC是⊙的直径，AB=AC=6，OE//AD。

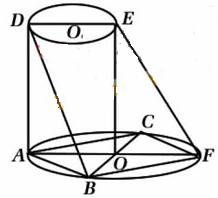
    （Ⅰ）求二面角B-AD-F的大小；

    （Ⅱ）求直线BD与EF所成的角。

解答

重庆卷(理)

（19）（本小题满分13分）

如图，在四棱锥中，底面，为直角，

，、分别为、CD的中点。

（Ⅰ）试证：平面；

（Ⅱ）设PA=K·AB，且二面角的平面角大于，求的取值范围。

                                 解答

山东卷(理)

19.(本小题满分12分)

   如图，已知平面A₁B₁C₁平行于三棱锥V-ABC的底面ABC，等边△AB₁C

所在的平面与底面ABC垂直，且∠ACB＝90°．设AC＝2a，BC＝a．

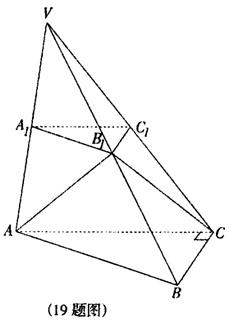
   (Ⅰ)求证直线B₁C₁是异面直线AB₁与A₁C₁的公垂线；

   (Ⅱ)求点A到平面VBC的距离；

   (Ⅲ)求二面角A-VB-C的大小．

解答

江西卷(理)

19．(本小题满分12分)

     如图，已知△ABC是边长为1的正三角形，M、N分别是边AB、AC上的

   点，线段MN经过△ABC的中心G.设∠MGA=α(≤α≤)．

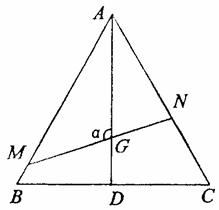
   (1)试将△AGM、△AGN的面积(分别记为S₁与S₂)表示为α的函数；

   (2)求y=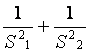的最大值与最小值．

解答

 陕西卷(理)

（１９）（本小题满分１２分）

如图，点A在直线上的射影为点B在上的射影为

已知求：

       （I）直线AB分别与平面所成角的大小；

       （II）二面角的大小。

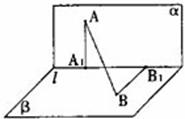
(第19题图)

解答

 四川卷(理)

（19）（本大题满分12分）

某课程考核分理论与实验两部分进行，每部分考核成绩只记“合格”与

“不合格”，两部分考核都是“合格”则该课程考核“合格”，甲、乙、

丙三人在理论考核中合格的概率分别为；在实验考核中合格的概

率分别为，所有考核是否合格相互之间没有影响

（Ⅰ）求甲、乙、丙三人在理论考核中至少有两人合格的概率；

（Ⅱ）求这三人该课程考核都合格的概率。（结果保留三位小数）

解答

 安徽卷(理)

（19）（本小题满分12分）

如图，P是边长为1的正六边形ABCDDEF所在平面外一点，PA=1，P在平面ABC内的

射影为BF的中点O。

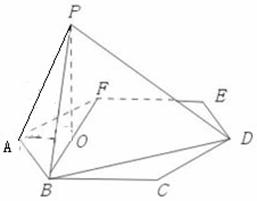
（Ⅰ）证明PA┴BF：

（Ⅱ）求面APB与面DPB所成二面角的大小。

解答