福建(理)
一、选择题(每题5分)
(2)在等差数列![]() 中,已知
中,已知![]() 则
则![]() 等于(
)
等于(
)
(A)40 (B)42 (C)43 (D)45
三、解答题
(22)(本小题满分14分)
已知数列![]() 满足
满足![]()
(I)求数列![]() 的通项公式;
的通项公式;
(II)
若数列|bn|满足![]() ,
,
证明:|bn|是等差数列
(Ⅲ)证明: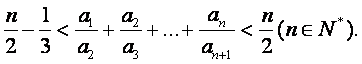
浙江(理)
一、选择题(每小题5分)
(8)若多项式![]() ,则
,则![]()
(A)9 (B)10 (C)-9 (D)-10
二、填空题(每小题4分)
(11)设![]() 为等差数列{
为等差数列{![]() }的前n项和,若
}的前n项和,若![]()
则公差为 ____________(用数字作答)。 解答
天津(理)
一、选择题(每小题5分)
(7)已知数列{an}、{bn}都是公差为1的等差数列,其首项分别为al、bl,
且a1+b1=5,a1、b1∈N*.设cn=![]() (n∈N*),则数列{cn}的前10项和
(n∈N*),则数列{cn}的前10项和
等于()
(A)55 (B)70 (C)85 (D)100
二、填空题(每小题4分)
(11)(2x+![]() )7的二项展开式中x的系数是_________(用数字作答).
)7的二项展开式中x的系数是_________(用数字作答).
三、解答题
(21)(本小题满分14分)
已知数列{xn}、{yn}满足x1=x2=1,y1=y2=2,并且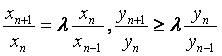
(![]() 为非零参数,n=2,3,4,…).
为非零参数,n=2,3,4,…).
(Ⅰ)若x1、x3、x5成等比数列,求参数![]() 的值;
的值;
(Ⅱ)当![]() >0时,证明
>0时,证明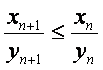 (n∈N*);
(n∈N*);
(Ⅲ)当![]() >1时,证明
>1时,证明 <
<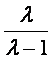 (n∈N*).
(n∈N*).
江苏
一、选择题(每小题5分)
(5)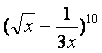 的展开式中含x的正整数指数幂的项数是
的展开式中含x的正整数指数幂的项数是
(A)0 (B)2 (C)4 (D)6
二、填空题(每小题5分)
(15)对正整数n,设曲线![]() 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为![]() ,
,
则数列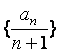 的前n项和的公式是
解答
的前n项和的公式是
解答
三、解答题
(21)(本小题满分14分)
设数列![]() 、
、![]() 、
、![]() 满足:
满足:![]() ,
,![]() (n=1,2,3,…),
(n=1,2,3,…),
证明![]() 为等差数列的充分必要条件是
为等差数列的充分必要条件是![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)
(n=1,2,3,…)
辽宁(理)
一、选择题(每题5分)
(9)
在等比数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,若数列
,若数列![]() 也是等比数列,
也是等比数列,
则![]() 等于(
)
等于(
)
(A)![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)![]()
重庆(理)
一、选择题(每小题5分)
(2)在等差数列![]() 中,若
中,若![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,
则![]() 的值为(
)
的值为(
)
(A)48 (B)54 (C)60 (D)66
(5)若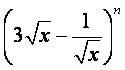 的展开式中各项系数之和为64,则展开式的常数项为()
的展开式中各项系数之和为64,则展开式的常数项为()
(A)-540 (B)-162 (C)162 (D)540
二、填空题(每小题4分)
(14)在数列![]() 中,若
中,若![]() ,
,![]() ,则该数列的通项
,则该数列的通项![]() 。
。
湖南(理)
一、选择题(每题5分)
2.若数列{an}满足:a1=![]() ,且对任意正整数m,n都有am+n=am·an,
,且对任意正整数m,n都有am+n=am·an,
则![]() (a1+a2+…+an)=(
)
(a1+a2+…+an)=(
)
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
湖北(理)
一、选择题(每题5分)
2.若互不相等的实数a、b、c成等差数列,c、a、b成等比数列,且a+3b+c=10,
则a=( )
A.4 B. 2 C. -2 D. -4
广东
一、选择题(每题5分)
6.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,
则其公差为()
A.5 B.4 C.3 D.2
13.在(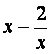 )11的展开式中,x5的系数为_____________。
)11的展开式中,x5的系数为_____________。
三、解答题
19.(本小题满分14分)
已知公比为q(0<q<1)的无穷等比数列{an}各项的和为9,无穷等比
数列{an2}各项的和为![]() 。
。
(Ⅰ)求数列{an}的首项a1和公比q:
(Ⅱ)对给定的k(k=1,2,…,n),设T{k}是首项为ak,公差为2ak-1的
等差数列,求数列T{2}的前10项之和:
(Ⅲ)设bi为数列![]() 的第i项,sn=b1+b2+…+bn,求sn,并求正整数
的第i项,sn=b1+b2+…+bn,求sn,并求正整数
m(m>1),使得![]()
![]() 存在且不等于零。
存在且不等于零。
(注:无穷等比数列各项的和即当n![]() 时该无穷等比数列前n项和的极限)
时该无穷等比数列前n项和的极限)
北京(理)
一、 选择题(每题5分)
(7)设f(n)=2+24+27+210+…+23n+10(n∈N),则f(n)等于( )
(A)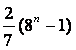 (B)
(B)![]() (8n+1-1)
(8n+1-1)
(C)![]() (8n+3-1)
(D)
(8n+3-1)
(D)![]() (8n+4-1)
(8n+4-1)
三、解答题
(20)(本小题共14分)
在数列{an}中,若a1,a2是正整数,且an=|an-1-an-2|,n=3,4,5,…,
则称{an}为“绝对差数列”.
(Ⅰ)举出一个前五项不为零的“绝对差数列”(只要求写出前十项);
(Ⅱ)若“绝对差数列”{an}中,a20=3,a21=0,数列{bn}满足bn=an+ an+1
+ an+2,n=1,2,3,…,分别判断当n→∞时,an与bn的极限是否存在,如果存
在,求出其极限值;
(Ⅲ)证明:任何“绝对差数列”中总含有无穷多个为零的项.
上海(理)
三、解答题
21.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,
第3小题满分6分)
已知有穷数列![]()
![]()
![]() 共有2
共有2![]() 项(整数
项(整数![]() ≥2),首项
≥2),首项![]() =2.设该数列的前
=2.设该数列的前![]() 项
项
和为![]() ,且
,且![]() =
=![]() +2(
+2(![]() =1,2,┅,2
=1,2,┅,2![]() -1),其中常数
-1),其中常数![]() >1.
>1.
(1)求证:数列![]()
![]()
![]() 是等比数列;
是等比数列;
(2)若![]() =2
=2![]() ,数列
,数列![]()
![]()
![]() 满足
满足![]() =
=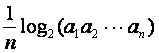 (
(![]() =1,2,┅,2
=1,2,┅,2![]() ),
),
求数列![]()
![]()
![]() 的通项公式;
的通项公式;
(3)若(2)中的数列![]()
![]()
![]() 满足不等式
满足不等式
|![]() -
-![]() |+|
|+|![]() -
-![]() |+┅+|
|+┅+|![]() -
-![]() |+|
|+|![]() -
-![]() |≤4,求
|≤4,求![]() 的值.
的值.
山东(理)
一、选择题(每小题5分)
10.已知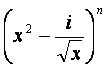 的展开式中第三项与第五项的系数之比为-
的展开式中第三项与第五项的系数之比为-![]() ,
,
其中i2=-1,则展开式中常数项是()
(A)-45i (B)45i (C)-45 (D)45
三、解答题
22.(本小题满分14分)
已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n=1,2,3,….
(Ⅰ)证明数列{lg(1+an)}是等比数列;
(Ⅱ)设Tn=(1+a1)(1+a2)…(1+an),求Tn及数列{an}的通项;
(Ⅲ)记bn=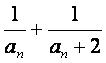 ,求数列{bn}的前n项和Sn,并证明Sn+
,求数列{bn}的前n项和Sn,并证明Sn+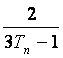 =1.
=1.
江西(理)
一、选择题(每题5分)
7.已知等差数列{an}的前n项和Sn,若![]() =a1
=a1![]() +a200
+a200![]() ,且A、B、C
,且A、B、C
三点共线(该直线不过点O),则S200等于( )
A.100 B.101 C.200 D.201
二、填空题(每题4分)
13.数列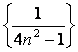 的前n项和为Sn,则
的前n项和为Sn,则![]() Sn=________.
Sn=________.
三、解答题
22.(本小题满分14分)
已知数列{an}满足:a1=![]() ,且an=
,且an= (n≥2,n∈N*).
(n≥2,n∈N*).
(1)求数列{an}的通项公式;
(2)证明:对一切正整数n,不等式a1·a2·…·an<2·n!恒成立.
陕西(理)
二、填空题(每小题4分)
14. 展开式中
展开式中![]() 的常数项为_____(用数字作答)。解答
的常数项为_____(用数字作答)。解答
三、解答题
(20)(本小题12分)
已知正项数列![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() 且
且![]() 成等比
成等比
数列,求数列![]() 的通项
的通项![]()
安徽(理)
三、解答题
(21)(本小题满分12分)
数列![]() 的前n项和为Sn,已知
的前n项和为Sn,已知![]() ,sn=n2an-n(n-1),n=1,2…
,sn=n2an-n(n-1),n=1,2…
(Ⅰ)写出sn与![]() 的递推关系式(n
的递推关系式(n![]() 2),并求sn关于n的表达式:
2),并求sn关于n的表达式:
(Ⅱ)设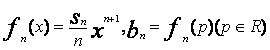 求数列{bn}的前n项和Tn。
求数列{bn}的前n项和Tn。
四川(理)
三、解答题
(20)(本大题满分12分)
已知数列![]() ,其中
,其中![]() ,记数列
,记数列![]() 的前
的前![]() 项
项
和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]()
(Ⅰ)求![]() ;
;
(Ⅱ)设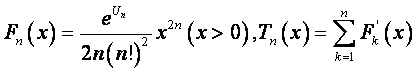 ,
,
(其中![]() 为
为![]() 的导函数),计算
的导函数),计算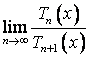
全国卷(Ⅰ)理
一、选择题(每题5分)
(10)设{an}是公差为正数的等差数列,若a1+a2+a3=15,a1a2a3=80
则a11+a12+a13=( )
(A)120 (B)105 (C)90 (D)75
三、解答题
(22)(本小题满分12分)
设数列{an}的前n项和
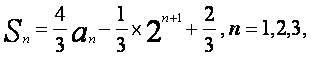 …。
…。
(Ⅰ)求首项a1与通项an;
(Ⅱ)设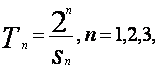 …,证明:
…,证明: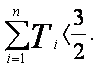
全国卷(Ⅱ)理
一、选择题(每小题5分)
(11)设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若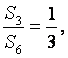 则
则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题(每小题4分)
(13)在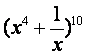 的展开式中常数项是_____。(用数字作答)
的展开式中常数项是_____。(用数字作答)
三、解答题
(22)(本小题满分12分)
设数列![]() 的前
的前![]() 项和为
项和为![]() ,且方程
,且方程
![]()
有一根为![]()
(I)求![]()
(II)求![]() 的通项公式
的通项公式