三、解答题

22.(本小题满分14分)

    已知a1＝2，点(an，an+1)在函数f(x)=x2+2x的图象上，其中n=1，2，3，…．

(Ⅰ)证明数列{lg(1+an)}是等比数列；

(Ⅱ)设Tn=(1+a1)(1+a2)…(1+an)，求Tn及数列{an}的通项；

(Ⅲ)记bn=，求数列{bn}的前n项和Sn,并证明Sn+=1.

解：(Ⅰ)由已知  an+1＝a2n+2an，

        ∴an+1+1＝(an+1)2

        ∵a1=2

        ∴an+1＞1，两边取对数得：                                                       

        lg(1+an+1)=2 lg(1+an)，

        即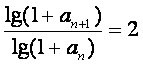

        ∴{lg(1+an)}是公比为2的等比数列.

    (Ⅱ)由(Ⅰ)知  lg(1+an)=2n-1·lg(1+a1)

                          =2n-1·lg3

                          =lg3

        ∴1+an＝3.              (*)

        ∴Tn=(1+a1)(1+a2)…(1+an)

           =3·3·3·…·3

           =

           =3

        由(*)式得an＝3-1．

  (Ⅲ)∵an+1=a2n+2an

      ∴an+1=an(an+2)

      ∴

      ∴

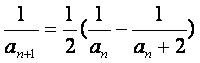
      又  bn=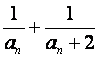

      ∴bn=2()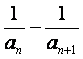

      ∴Sn=b1+b2+…+bn

          =2

      =2()

      ∵an=3-1，    a1＝2，    an+1=3-1

      ∴Sn＝1-

      又Tn＝

      ∴Sn+

　

　

　

　

　

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。