三、解答题

（21）（本小题满分12分）

数列的前n项和为S_n，已知，s_n=n²a_n-n(n-1),n=1，2…

（Ⅰ）写出s_n与的递推关系式（n2）,并求s_n关于n的表达式：

（Ⅱ）设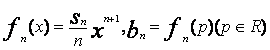求数列｛b_n｝的前n项和T_n。

   本小题主要考查等差、等比数列的基本知识，考查分析问题和归纳推理能力。满分12分。

（Ⅰ）解法1：当时，，即

        ①

已知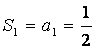，由递推关系式可得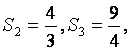

由此，可猜想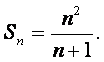：②

下面用数学归纳法证明②式：

证明：（i）当时，由条件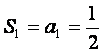，又②式的右边等于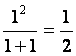，所以②式成立.

（ii）假设时，②式成立，即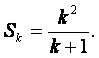

则当时，

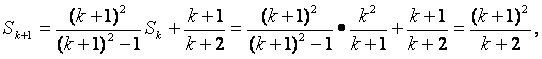
故当n=k+1时，②式也成立。

由（i），（ii）知，对一切正整数n, ②式成立.

解法2：当n≥2时，

即        

于是        .

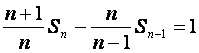∴{}是首项为1、公差为1的等差数列。

因而=1+（n-1）=n，故.

（Ⅱ）解：∵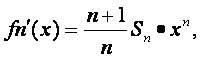

∴

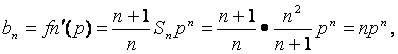
∴                  ③

当p=0时，=0；

当p=1时，

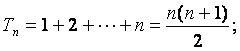
当时，在③式两边同乘以p，得到

                   ④

③—④得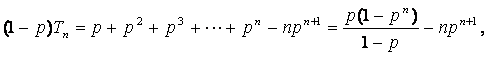

∴

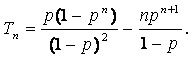
综上所述：