|
空间向量数量积运算的应用<-->空间向量的坐标表示
空间向量基本定理
①空间向量基本定理:
Ⅰ、空间向量基本定理:如果 是空间中三个不共面的单位向量,那么对于空间中任意一个向量 是空间中三个不共面的单位向量,那么对于空间中任意一个向量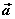 ,存在一个唯一的有序实数组 ,存在一个唯一的有序实数组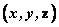 ,使得 ,使得
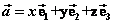 。 。
Ⅱ、定理说明:
⑴不共面向量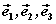 叫做表示空间中所有向量的一组基底, 叫做表示空间中所有向量的一组基底,
基底不唯一,关键是不共面;
⑵由空间向量基本定理可将空间中任一向量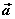 在给定基底 在给定基底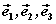 的 的
条件下进行分解,分解的形式是唯一的。
②空间向量的正交分解:
Ⅰ、关于向量的夹角:
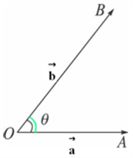 如图,已知两个非零向量a和b,作 如图,已知两个非零向量a和b,作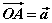 , ,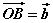 , ,
则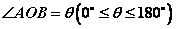 叫做向量 叫做向量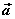 与 与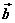 的夹角。 的夹角。
显然,当θ=0°时,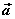 与 与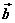 同向;当θ=180°时, 同向;当θ=180°时,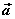 与 与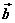 反向。因此,两非零 反向。因此,两非零
向量的夹角在区间[0°,180°]内。
Ⅱ、垂直向量:如果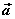 与 与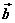 的夹角是90°,则说向量 的夹角是90°,则说向量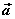 与 与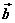 垂直,记作 垂直,记作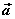 ⊥ ⊥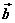 。 。
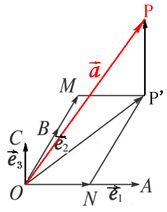
Ⅲ、空间向量的正交分解:
如果 是空间中三个两两垂直的单位向量, 是空间中三个两两垂直的单位向量,
那么对于空间中任意一个向量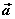 ,存在一个唯一的有序实数组 ,存在一个唯一的有序实数组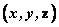 ,使 ,使
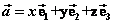 。 。
这样把空间中任意一个向量分解为三个两两垂直的向量,叫做空间向量的正交分解。
空间向量的正交分解是空间向量分解中非常重要的一种情形,它构建了空间向量及运算的坐标表示。
空间向量数量积运算的应用<-->空间向量的坐标表示
全网搜索"空间向量基本定理"相关
|

