|
空间向量的减法运算<-->空间向量数量积运算
空间向量的数乘运算
⑴空间向量数乘运算定义:
我们规定实数λ与向量 的积是一个向量,这种运算叫做向量的数乘,记作 的积是一个向量,这种运算叫做向量的数乘,记作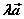 。它的长度与方向规定如下: 。它的长度与方向规定如下:
1o 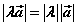 ; ;
2o 当λ>0时,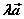 的方向与 的方向与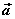 的方向相同;当λ<0时, 的方向相同;当λ<0时,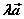 的方向与 的方向与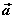 的方向相反;当λ=0时, 的方向相反;当λ=0时,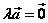 。 。
⑵空间向量数乘运算的几何意义:平面向量数乘运算的几何意义是把向量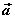 沿 沿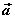 的方向或 的方向或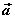 的反方向放大或缩小。 的反方向放大或缩小。
⑶空间向量数乘运算律:
设λ、μ为实数,那么
1o 对实数的结合律:  ; ;
2o 对实数加法的分配率: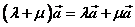 ; ;
3o 对向量加法的分配率: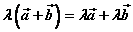 。 。
⑷空间向量共线定理:如果向量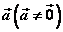 与 与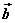 共线(或说 共线(或说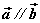 ),那么有且只有一个实数λ,使 ),那么有且只有一个实数λ,使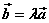 。 。
⑸直线的方向向量:如果向量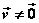 与直线 与直线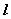 平行,则称向量 平行,则称向量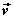 为直线 为直线 的方向向量。 的方向向量。
⑹空间向量数乘运算的坐标表示:
若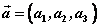 ,则 ,则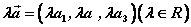 。 。
即实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标。
|

