|
曲线的方程与方程的曲线<-->空间向量的概念
求曲线的方程
①求未知曲线的方程:
求未知曲线的方程常用轨迹法,即把曲线上动点的几何条件解析化的方法。常见的方法有直接法,定义法,参数法,相关点法(代入法),交轨法等。
Ⅰ、直接法:直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程。
程序:
—建立坐标系,设动点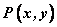 ; ;
—揭示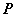 的几何条件 的几何条件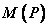 ; ;
—将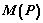 解析化; 解析化;
—化简方程;
—注意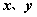 范围的制约。 范围的制约。
Ⅱ、定义法:若动点轨迹的条件符合某一基本轨迹的定义(如椭圆、双曲线、抛物线、圆等),构建已知轨迹定义的几何特征,利用相应的轨迹定义直接探求其方程。.
程序:
—建立坐标系,设动点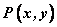 ; ;
—揭示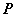 的几何条件 的几何条件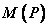 ; ;
—说明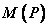 是某一已知轨迹的定义; 是某一已知轨迹的定义;
—求出已知轨迹的方程;
—注意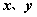 范围的制约。 范围的制约。
Ⅲ、代入法(相关点法):若两个或两个以上动点之间相关,根据相关点所满足的方程,通过转换代入而求动点的轨迹方程。
程序:设已知动点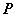 与定曲线 与定曲线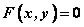 上的动点 上的动点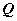 的关系,则 的关系,则
—设动点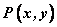 , , ; ;
—建立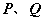 间的坐标关系; 间的坐标关系;
—解得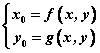 ; ;
—把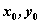 代入方程 代入方程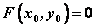 得 得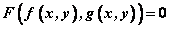 ; ;
—化简方程;
—注意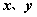 范围的制约。 范围的制约。
Ⅳ、参数法:若动点的坐标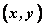 中的 中的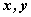 分别随第三个变量的变化而变化,我们可以设这个变量为参数,建立轨迹的参数方程,消去参数得曲线的轨迹方程。 分别随第三个变量的变化而变化,我们可以设这个变量为参数,建立轨迹的参数方程,消去参数得曲线的轨迹方程。
程序:
—设动点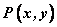 ; ;
—根据动点的运动变化特点选择参数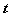 ,确定 ,确定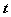 的取值集合 的取值集合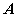 ; ;
—建立动点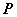 的坐标 的坐标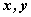 与参数 与参数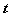 的函数关系 的函数关系
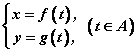 ; ;
—消去参数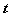 得 得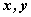 直接关系的方程; 直接关系的方程;
—化简方程;
—注意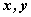 范围的制约。 范围的制约。
Ⅴ、交轨法:若两条曲线系相交,那么联立、消参、化简得两条曲线系交点的轨迹方程。
程序:
—设两条动曲线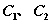 的交点为 的交点为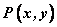 ; ;
—揭示两条曲线系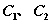 的方程分别为 的方程分别为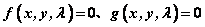 ; ;
—联立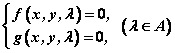 ; ;
—消去参数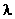 得 得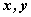 直接关系的方程; 直接关系的方程;
—化简方程;
—注意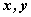 范围的制约。 范围的制约。
②求已知曲线的方程:
求已知曲线的方程即求已知轨迹定义的曲线方程,其实质就是用待定系数法确定已知轨迹定义的曲线方程。
待定系数法程序:
—设含待定系数的已知曲线方程;
—依独立条件列含待定系数的方程组;
—解方程组,求得待定的系数;
—写出所求的曲线方程;
—注意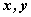 范围的制约。 范围的制约。
③求轨迹方程的说明:
Ⅰ、涉及圆锥曲线的轨迹方程,用圆锥曲线的定义方法解题能简化解题过程;
Ⅱ、多个动点的轨迹方程问题,用相关点法或参数法求解较好;
Ⅲ、解决轨迹问题要注意曲线上的点和方程的解之间的“等价关系”,曲线上的点的范围或方程解的范围既不能缩小也不能扩大,注意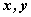 范围的制约。即一定要注意轨迹的纯粹性和完备性,要注意区别“轨迹”与“轨迹方程”是两个不同的概念。 范围的制约。即一定要注意轨迹的纯粹性和完备性,要注意区别“轨迹”与“轨迹方程”是两个不同的概念。
|

