|
双曲线的方程<-->双曲线与点的位置关系
双曲线的几何性质
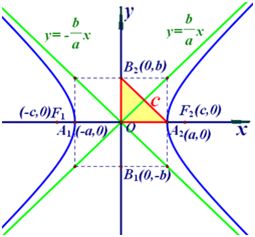
①双曲线的范围
由双曲线标准方程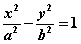 ,双曲线上点的坐标 ,双曲线上点的坐标 满足不等式 满足不等式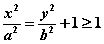 , ,
∴ 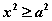 , ∴ , ∴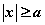 ,得 ,得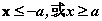 , ,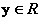 。 。
这表明双曲线位于两直线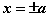 的外侧区域里。 的外侧区域里。
②双曲线的对称性
在双曲线标准方程里,以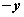 代替 代替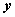 方程不变,所以若点 方程不变,所以若点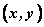 在曲线上时,则点 在曲线上时,则点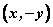 也在曲线上,所以曲线关于 也在曲线上,所以曲线关于 轴对称; 轴对称;
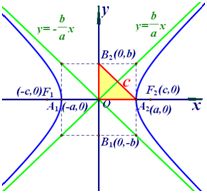
同理,以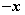 代替 代替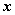 方程不变,则曲线关于 方程不变,则曲线关于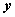 轴对称;同时以 轴对称;同时以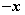 代替 代替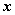 , ,
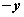 代替 代替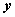 方程也不变,则曲线关于原点对称。 方程也不变,则曲线关于原点对称。
所以,双曲线关于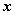 轴、 轴、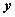 轴和原点对称。这时,坐标轴是双曲线的对称轴,原点是对称中心,双曲线的对称中心叫双曲线的中心。 轴和原点对称。这时,坐标轴是双曲线的对称轴,原点是对称中心,双曲线的对称中心叫双曲线的中心。
③双曲线的顶点
确定曲线在坐标系中的位置,常需要求出曲线与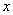 轴、 轴、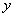 轴的交点坐标。 轴的交点坐标。
在双曲线的标准方程中,令 , , 的值不存在,则双曲线与 的值不存在,则双曲线与 轴无交点。令 轴无交点。令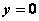 得 得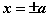 ,即 ,即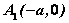 , , 是双曲线与 是双曲线与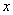 轴的两个交点。这两个交点叫做双曲线的顶点。 轴的两个交点。这两个交点叫做双曲线的顶点。
记 , ,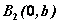 ,则线段 ,则线段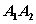 叫做双曲线的实轴,它的长等于 叫做双曲线的实轴,它的长等于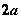 , ,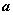 叫做双曲线的实半轴长;线段 叫做双曲线的实半轴长;线段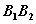 叫做双曲线的虚轴,它的长等于 叫做双曲线的虚轴,它的长等于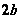 , ,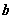 叫做双曲线的虚半轴长。 叫做双曲线的虚半轴长。
.若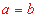 ,那么双曲线叫做等轴双曲线,其中 ,那么双曲线叫做等轴双曲线,其中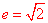 ,渐近线 ,渐近线 . .
若以已知双曲线的虚轴为实轴,以实轴为虚轴的双曲线叫做原双曲线的共轭双曲线。
④双曲线的定型三角形
由双曲线的对称性知,双曲线的虚轴端点到顶点的距离为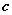 ,那么虚轴端点、顶点和中心三点构成双曲线的定型直角三角形,可称之为双曲线的定型三角形。 ,那么虚轴端点、顶点和中心三点构成双曲线的定型直角三角形,可称之为双曲线的定型三角形。
即在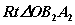 中, 中, 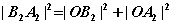 ,即 ,即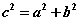 。 。
⑤双曲线的离心率
双曲线的焦距与长轴的比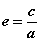 叫双曲线的离心率。 叫双曲线的离心率。
∵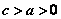 ,∴ ,∴ 。由 。由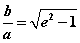 知, 知,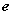 越接近 越接近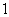 , ,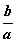 就越小,对应的双曲线张口越小; 就越小,对应的双曲线张口越小;
反之,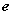 越大, 越大,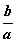 就越大,对应的双曲线张口越大。 就越大,对应的双曲线张口越大。
⑥双曲线的渐近线
Ⅰ、焦点在x轴:双曲线 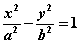 的渐近线为 的渐近线为
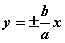 ,或 ,或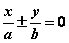 ,或 ,或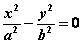 。 。
Ⅱ、焦点在y轴:双曲线 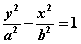 的渐近线为 的渐近线为
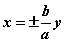 ,即 ,即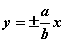 ,或 ,或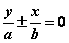 ,或 ,或 。 。
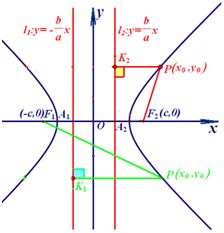
⑦双曲线的焦半径
若 是双曲线 是双曲线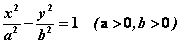 上任一点, 上任一点,
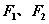 是双曲线的左焦点和右焦点,则双曲线的焦半径为 是双曲线的左焦点和右焦点,则双曲线的焦半径为
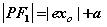 , ,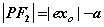 ; ;
若 是双曲线 是双曲线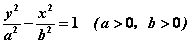 上任一点, 上任一点,
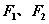 是双曲线的下焦点和上焦点,则双曲线的焦半径为 是双曲线的下焦点和上焦点,则双曲线的焦半径为
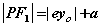 , ,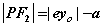 。 。
⑧双曲线的准线
当点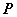 到定点 到定点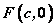 的距离和它到定直线 的距离和它到定直线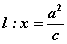 的距离的比是常数 的距离的比是常数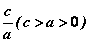 时,这个点的轨迹是双曲线,同样得到双曲线的标准方程 时,这个点的轨迹是双曲线,同样得到双曲线的标准方程 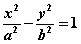 (其中 (其中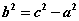 )。这条定直线叫双曲线的准线。 )。这条定直线叫双曲线的准线。
根据图形的对称性,双曲线有两条准线,对于中心在原点,焦点在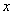 轴上的双曲线,与焦点 轴上的双曲线,与焦点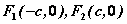 对应的准线方程分别为 对应的准线方程分别为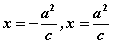 ; ;
对于中心在原点,焦点在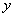 轴上的双曲线,与焦点 轴上的双曲线,与焦点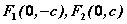 对应的准线方程分别为 对应的准线方程分别为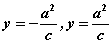 。 。
|

