|
函数奇偶性的判定方法<-->利用函数性质画图象--重要步骤
函数奇偶性的应用
①判断函数的奇偶性:按判定方法操作,一般先用图象法,也可以用定义法,或运算法、复合法,因题而异。
②证明函数的奇偶性:一定要用定义法证明。
③利用函数的奇偶性求函数解析式:
已知定义域一边对称区间上的函数解析式,利用函数的奇偶性可求得另一边对称区间上的函数解析式,进而求得整个函数解析式。即
已知定义在R上奇函数,若当x∈(-∞,0]时,函数解析式为y=f(x),则R上的函数解析式为
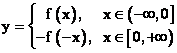 。 。
已知定义在R上偶函数,若当x∈(-∞,0]时,函数解析式为y=f(x),则R上的函数解析式为
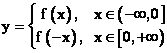 。 。
④求值域与最值:
⑴求值域:
Ⅰ、已知定义域一边对称区间上的函数值范围,利用函数的奇偶性可求得另一边对称区间上的函数值范围,进而求得整个定义域上的函数值范围,即求得整个函数的值域。
Ⅱ、已知定义在R上奇函数,若当x∈(-∞,0]时,函数值的范围为[a,b],则当x∈[0,+∞)时,函数值的范围为[-b,-a],所以在R上的函数值域为[-b,-a]∪[a,b]。
Ⅲ、已知定义在R上偶函数,若当x∈(-∞,0]时,函数值的范围为[a,b],则当x∈[0,+∞)时,函数值的范围为[a,b],所以在R上的函数值域为[a,b]。
⑵求最值:同理
已知定义域一边对称区间上的函数值范围,利用函数的奇偶性可求得另一边对称区间上的函数值范围,进而求得整个定义域上的函数值范围,即可求得整个函数的最值。
已知定义在R上奇函数,若当x∈(-∞,0]时,函数的最大(小)值A,当x∈[0,+∞)时,函数的最小(大)值为-A,所以在R上的函数的最小(大)值为-A, 最大(小)值A。
已知定义在R上偶函数,若当x∈(-∞,0]时,函数的最大值A,最小值B,则当x∈[0,+∞)时,函数的最大值也是A,最小值也是B,所以在R上的函数的最大值为A, 最小值为B。
函数奇偶性的判定方法<-->利用函数性质画图象--重要步骤
全网搜索"函数奇偶性的应用"相关
|

