|
函数奇偶性的几何特征<-->函数奇偶性的应用
函数奇偶性的判定方法
奇偶性的判断方法有图象法,定义法,运算法和复合法。证明函数奇偶性一定要用定义法。
①图象法:
若函数图象关于原点成中心对称,则其函数是奇函数;若函数图象关于y轴对称,则其函数是偶函数。
②定义法:
Ⅰ、定义域是否关于原点对称,若不是,则是非奇非偶函数;若是,还要看Ⅱ。
Ⅱ、若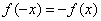 ,或 ,或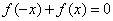 ,或 ,或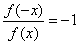 (若f(x)≠0),则是奇函数; (若f(x)≠0),则是奇函数;
若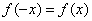 ,或 ,或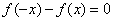 ,或 ,或 (若f(x)≠0),则是偶函数。 (若f(x)≠0),则是偶函数。
③运算法:
设f(x),g(x)的定义域分别是D1 ,D2 ,那么在它们的公共定义域上奇偶性:
奇+奇=奇,奇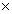 奇=偶,偶+偶=偶,偶 奇=偶,偶+偶=偶,偶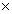 偶=偶,奇 偶=偶,奇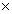 偶=奇。 偶=奇。
④复合法:
已知函数g(x),f(x),f[g(x)]的定义域都是关于原点对称的,
若u=g(x),y=f(u)都是奇函数时,则y=f[g(x)]是奇函数;
若u=g(x),y=f(u)都是偶函数,或者一奇一偶时,则y= f[g(x)]是偶函数。
|

