|
函数单调性的应用——求极值<-->函数奇偶性定义
函数单调性的应用——求最值
Ⅰ、最值定义:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
⑴对于任意的x∈I,都有f(x)≤M;
⑵存在xo ∈I,使得f(xo )=M.
那么,称M是函数y=f(x)的最大值。
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
⑴对于任意的x∈I,都有f(x)≥M;
⑵存在xo ∈I,使得f(xo )=M.
那么,称M是函数y=f(x)的最小值。
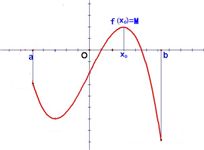 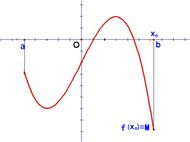
Ⅱ、方法1:
若函数y=f(x)在定义域 [a,b] 上递增,则函数的最大值为f(b),最小值为f(a) ;
若函数y=f(x)在定义域 [a,b] 上递减,则函数的最大值为f(a),最小值为f(b)。
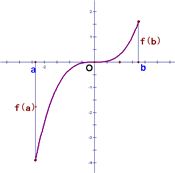 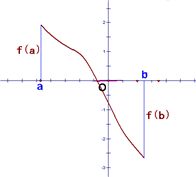
Ⅲ、方法2:
若函数y=f(x)在定义域 [a,b] 上连续,则
①求函数y=f(x)在(a,b)内的极值;
②求函数在端点的函数值f(a),f(b);
③将函数y=f(x)的个极值与端点函数值f(a),f(b)比较,其中最大的一个为最大值,最小的一个为最小值。
如图,定义在[a,b]上的连续函数y=f(x),求得极值为f(x1 )、f(x2 ),求得定义域端点的函数值为f(a)、f(b),则函数的最大值与最小值分别为
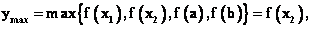
 。 。

函数单调性的应用——求极值<-->函数奇偶性定义
全网搜索"函数单调性的应用——求最值"相关
|

