|
有关函数单调性的定理<-->函数单调性证明方法
最大值和最小值
最大值:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
1 对于任意的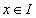 ,都有 ,都有 ; ;
2 存在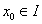 ,使得 ,使得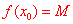 ,那么我们称M是函数y=f(x)的最大值。 ,那么我们称M是函数y=f(x)的最大值。
最小值:一般地,设函数y=f(x)的定义域为I,如果存在实数m满足:
⑴对于任意的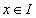 ,都有 ,都有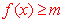 ; ;
⑵存在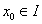 ,使得 ,使得 ,那么我们称m是函数y=f(x)的最小值。 ,那么我们称m是函数y=f(x)的最小值。
详解:求函数最值的常用方法和求函数值域的方法基本上是相同的,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值,因此求函数的最值与值域,其实质是相同的,只是提问的角度不同,因为答题的方式就有所差异。
函数的值域常常化归为求函数的最值问题,要重视函数的单调性在确定函数最值过程中的作用,特别是要重视实际问题最值的求法。
有关函数单调性的定理<-->函数单调性证明方法
全网搜索"最大值和最小值"相关
|

