|
最大值和最小值<-->判断函数单调性的方法
函数单调性证明方法
证明函数单调性的方法有:定义法(即比较法);导数法。
实际上,用导数方法证明一般函数单调性是很便捷的方法,定义法是基本方法,常用来证明解决抽象函数或不易求导的函数的单调性。
(1)定义法:利用增减函数的定义证明。在证明过程中,把数式的大小比较转化为求差比较(或求商比较)。
⑴转化为求差比较证明程序:
①设任意的x1 、x2 ∈D,使x1 <x2 ;
②求差—变形—判断正负;此为关键步骤,变形大多要“因式分解”。
求差: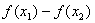 ; 变形:化简、因式分解; 判断: ; 变形:化简、因式分解; 判断: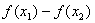 的符号正或负。 的符号正或负。
③下明确结论。
⑵转化为求商比较证明程序:
①设任意的x1 、x2 ∈D,使x1 <x2 (若0<x1 <x2 ,则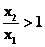 ;若x1 <x2 <0,则 ;若x1 <x2 <0,则 ); );
②求商—变形—判断小于或大于1;此为关键步骤,变形要注意“因式分解”。
求商: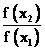 ; 变形:化简、因式分解; 判断: ; 变形:化简、因式分解; 判断: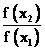 小于或大于1。 小于或大于1。
③下明确结论,要注意商的分母的正负,即
若
若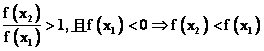 。 。
(2)导数法:利用函数单调性与可导函数的正负性关系证明。
设可导函数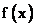 在定义域的某个区间(a,b)内,如果 在定义域的某个区间(a,b)内,如果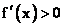 ,那么函数f(x)在这个区间内单调递增;如果 ,那么函数f(x)在这个区间内单调递增;如果 ,那么函数f(x)在这个区间内单调递减。 ,那么函数f(x)在这个区间内单调递减。
求导证明函数单调性的程序:
①求函数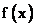 的导数 的导数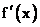 ; ;
②把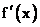 变形,化简,因式分解,判断正负; 变形,化简,因式分解,判断正负;
③下明确结论。
最大值和最小值<-->判断函数单调性的方法
全网搜索"函数单调性证明方法"相关
|

