|
判断是否函数关系的原则<-->函数的三要素
设$a$, $b$是两个实数，而且$a＜b$.我们规定：
(1)满足不等式$a \leqslant x \leqslant b$的实数x的集合叫做闭区间，表示为$[a,b]$；
(2)满足不等式$a < x < b$的实数$x$的集合叫做开区间，表示为$(a,b)$；
(3)满足不等式$a \leqslant x < b$或$a < x \leqslant b$的实数$x$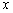 的集合叫做半开闭区间，表示为$[a,b)$或$(a,b]$。这里的实数$a$与$b$都叫做相应区间的端点。
详解：
函数区间有三类，分别是闭区间，开区间，半开闭区间。
实数集$R$可以用区间表示为$(-\infty,+\infty)$，“$\infty$”读作“无穷大”，“$-\infty$”读作“负无穷大”，“$+ \infty$”读作“正无穷大”。我们有
$x \geqslant a$ 表示为$[a,+\infty)$
$x>a$ 表示为$(a,+\infty)$
$x \leqslant b$ 表示为$(-\infty,b]$
$x <b$ 表示为$(-\infty,b)$.
判断是否函数关系的原则<-->函数的三要素
全网搜索"区间"相关
|
