|
子集的个数,真子集的个数,非空真子集的个数<-->交集及运算性质
并集:一般地,由所有属于集合$A$或属于集合$B$的元素组成的集合,称为集合$A$与$B$的并集,记作$A \cup B$(读作“$A$并$B$”),
即$A \cup B =\{x | x \in A,或 x \in B\}$.
用Venn图表示为:
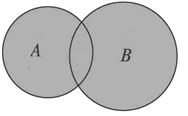 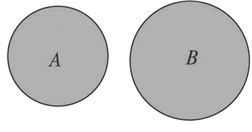
运算性质:
$A \cup B =B \cup A$,
$A \cup B \supseteq A$,
$A \cup U = U$,
$A \cup A =A$,
$A \cup \varnothing = A$.
子集的个数,真子集的个数,非空真子集的个数<-->交集及运算性质
全网搜索"并集及运算性质"相关
|

