|
23.1.3数形结合思想在解不等式中的应用<-->23.2.2不等式的证明的其他方法
23.2.1不等式的证明方法
(1)比较法
比较法是证明不等式的最基本、最重要的方法,它常用的证明方法有两种:
作差比较法:
①应用范围:当欲证的不等式两端是多项式、分式或对数式时,常用此法,
②方法:欲证A>B,只需证A-B>0.
③步骤:作差→变形(常用的变形方法有:通分因式分解,配方等)→判断(各因式大于或小于0)→结论(原不等式成立),其关键是分清题型进行合理变形.
④使用此法作差后主要变形形式的处理.
a.将差变形为常数或变形为一个常数或几个平方和的形式,常用配方法或实数特征$a^2≥0$判断差的符号.
b.将差变形为几个因式的积的形式,常用因式分解法.
总之,变形的主要目的是有利于判断式子的符号而变形方法不限定.也就是说,关键是变形的目标.如将差变形为$(a-b)(a^3-b^3)$也能判断它是正的,尽管它不是平方和的形式,也不是因式分解的结果.
c.若变形后得到二次三项式,常用判别式判定符号.
作商比较法:
①应用范围:当要证的式子两端是乘积的形式或幂、指数时,常用此法
②方法:要证A>B,常分以下三种情况:
若B>0,只需证明$\dfrac{A}{B} > 1$
若B=0,只需证明$A > 0$
若 B<0,只需证明$\dfrac{A}{B} < 1$
③步骤:作商一变形→判断(大于1或小于1)→结论.
(2)综合法
利用题设和某些已经证明过的不等式或不等式的性质推导出所要证明的不等式成立,这种证明方法称为综合法.
综合法的思路是“由因导果”也就是从已知的不等式出发,不断地用必要条件代替前面的不等式,直至推导出欲证的不等式.
(3)分析法
从所求证的不等式出发,分析使这个不等式成立的条件,只要使不等式成立的条件已具备,就断定原不等式成立,这种证明的方法叫做分析法.使用分析法时,要保证“后一步”是“前一步’的充分条件,通常采用“欲证-只需-已知”的格式.
分析法的思路是“执果索因”,在表述中经常用符号“←”这里要注意箭头的方向.用分析法时,一般用“←”,用综合法时,一般用“→”.
一般来说,无理不等式、三角不等式以及含绝对值符号的不等式,均以采用分析法较方便.
【小结】综合法与分析法的比较
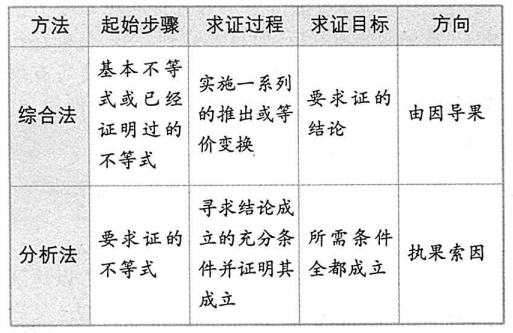
(4)反证法
要证不等式 M>N,先假设 M≤N,由题设及其他性质,推出矛盾,从而肯定M>N成立.凡涉及要证的不等式为否定性命题、唯一性命题或是含“至多”“至少”等字句时,可考虑使用反证法.
(5)放缩法
要证明不等式A<B成立,有时可以将它的一边放大或缩小,寻找一个中间量,如将A放大成C,即 A<C,后证C<B,这种证法叫放缩法.
常用的放缩技巧有:舍掉(或加进)一些项;在分式中放大或缩小分子或分母;应用基本不等式放缩. 如:
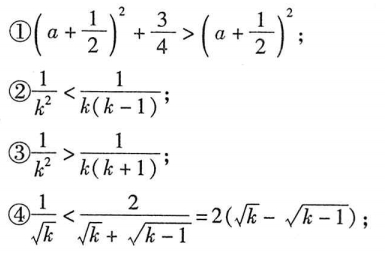

放缩法的理论依据主要有:不等式的传递性;
等量加不等量为不等量;
同分子(分母)异分母(分子)的两个分式大小的比较.
23.1.3数形结合思想在解不等式中的应用<-->23.2.2不等式的证明的其他方法
全网搜索"23.2.1不等式的证明方法"相关
|

