|
22.1.2平面直角坐标系中的伸缩变换<-->22.1.4柱坐标系
(1)极坐标系的概念
在平面内取一个定点$O$,从引一条射线,选定一个长度单位、一个角度单位以及计算角度的正方向(通常取逆时针方向为正方向),这样就建立了一个极坐标系,点叫做极点,射线叫做极轴。
极坐标系的四要素:极点,极轴,长度单位,角度单位和它的正方向,极坐标的四要素,缺一不可。
(2)点的极坐标
设$M$是平面内一点,极点$O$与点$M$的距离$|OM|$叫做点$M$的极径,记为$\rho$;以极轴$Ox$为始边,射线$OM$为终边的角$xOM$叫做点$M$的极角,记为$\theta$.有序数对$(\rho,\theta)$叫做点$M$的极坐标,如图.
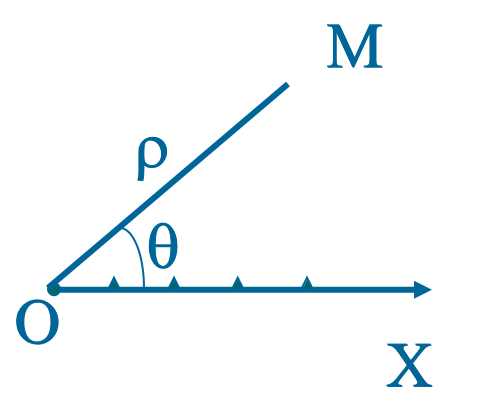
说明
①关于$\theta$和$\rho$的正负
极角$\theta$的始边是极轴,取逆时针方向为正,顺时针方向为负,$\theta$的值一般以弧度为单位。
$\rho >0$时,坐标为$(\rho,\theta)$的点$M$在极角$\theta$的终边上,$|OM|=\rho$;
$\rho <0$时,坐标为$(\rho,\theta)$的点$M$在极角$\theta$的终边的反向延长线上,$|OM|=-\rho$。
②特殊位置的点的极坐标



22.1.2平面直角坐标系中的伸缩变换<-->22.1.4柱坐标系
全网搜索"22.1.3极坐标系"相关
|

